


Next: About this document ...
Up: ARPACK Users' Guide: Solution
Previous: References
- logfil
- Obtaining Trace Output
- ndigit
- Obtaining Trace Output
- msaitr
- Obtaining Trace Output
- debug.h
- Obtaining Trace Output
- msaupd
- Obtaining Trace Output
- arpack_state
- Check Pointing ARPACK
- ex-sym.doc
- An Example for a
- ndigit
- Trace Debugging Capability
- logfil
- Trace Debugging Capability
- msaitr
- Trace Debugging Capability
-
- Stopping Criterion
- __aupd
- Naming Conventions, Precisions and
- __eupd
- Naming Conventions, Precisions and
- OP
- Reverse Communication Structure for
- dsaupd
- Computational Modes for Real
- dseupd
- Post-Processing for Eigenvectors Using dseupd
- dneupd
- Post-Processing for Eigenvectors Using dneupd
- znaupd
- Computational Modes for Complex
- zneupd
- Post-Processing for Eigenvectors Using zneupd
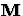 -inner product
-inner product
- Shift and Invert Spectral
-
- Shift and Invert Spectral
-
- Stopping Criterion
- _gemv
- Computational Routines
- XYaupd
- ARPACK subroutines
- XYeupd
- ARPACK subroutines
- XYaup2
- ARPACK subroutines
- Xgetv0
- ARPACK subroutines
- XYaitr
- ARPACK subroutines
- Xneigh
- ARPACK subroutines
- [s,d]seigt
- ARPACK subroutines
- XYgets
- ARPACK subroutines
- [s,d]Yconv
- ARPACK subroutines
- XYapps
- ARPACK subroutines
- Xortc
- ARPACK subroutines
- [s,d]ortr
- ARPACK subroutines
- [s,d]laqrb
- ARPACK subroutines
- [s,d]stqrb
- ARPACK subroutines
- XYaupd
- XYaupd
- XYaup2
- no title
- XYaitr
- XYaitr
- Xgetv0
- Xgetv0
- [s,d]neigh
- Xneigh
- [s,d]laqrb
- Xneigh
- [s,d]lahqr
- Xneigh
- [c,z]lahqr
- Xneigh
- [c,z]neigh
- Xneigh
- [c,z]trevc
- Xneigh
- [s,d]seigt
- [s,d]seigt
- [s,d]stqrb
- [s,d]seigt
- [s,d]stqr
- [s,d]seigt
- [s,d]Yconv
- [s,d]Yconv
- [c,z]naup2
- [s,d]Yconv
- XYapps
- XYapps
- XYeupd
- XYeupd
- Xtrsen
- XYeupd
- Xtrevc
- XYeupd
- Xtrmm
- XYeupd
- Xhseqr
- LAPACK routines used by
- Xlahqr
- LAPACK routines used by
- Xtrsen
- LAPACK routines used by
- [s,d]steqr
- LAPACK routines used by
- ctrevc
- LAPACK routines used by
- strevc
- LAPACK routines used by
- Xlahqr
- LAPACK routines used by
- Xgeqr2
- LAPACK routines used by
- sorm2r
- LAPACK routines used by
- cunm2r
- LAPACK routines used by
- Xlascl
- LAPACK routines used by
- Xlanhs
- LAPACK routines used by
- Xlacpy
- LAPACK routines used by
- Xlamch
- LAPACK routines used by
- [s,d]labad
- LAPACK routines used by
- [s,d]lapy2
- LAPACK routines used by
- Xlartg
- LAPACK routines used by
- [s,d]larfg
- LAPACK routines used by
- [s,d]larf
- LAPACK routines used by
- Xlaset
- LAPACK routines used by
- BLAS
- BLAS routines used by
- Xgemv
- BLAS routines used by
- [s,d]ger
- BLAS routines used by
- [c,z]geru
- BLAS routines used by
- Xaxpy
- BLAS routines used by
- Xscal
- BLAS routines used by
- [s,d]dot
- BLAS routines used by
- [c,z]dotc
- BLAS routines used by
- [cs,zd]scal
- BLAS routines used by
- [s,d]nrm2
- BLAS routines used by
- [sc,dz]nrm2
- BLAS routines used by
- Xcopy
- BLAS routines used by
- Xswap
- BLAS routines used by
-
- XYaup2
-
- XYaup2
-
- XYaup2
- COMMON
- Reverse Communication Interface
-
- [s,d]Yconv
- ido
- Reverse Communication Interface
- LR
- Regular Inverse Mode
- SR
- Regular Inverse Mode
- LI
- Regular Inverse Mode
- SI
- Regular Inverse Mode
- LM
- Regular Inverse Mode
- LI
- Regular Inverse Mode
- SI
- Regular Inverse Mode
- SR
- Regular Inverse Mode
- dssimp
- Directory Structure and Contents
- dssimp
- An Example for a
- XsdrvY
- Symmetric Drivers
- dsdrv1
- Standard Mode
- dsdrv2
- Shift-Invert Mode
- dsdrv3
- Regular Inverse Mode
- dsdrv4
- Shift-Invert Mode
- dsdrv5
- Buckling Mode
- dsdrv6
- Cayley Transformation Mode
- dndrv1
- Standard Mode
- dndrv2
- Shift-Invert Mode
- dndrv3
- Regular Inverse Mode
- dndrv4
- Spectral Transformations for Non-symmetric
- dndrv5
- Spectral Transformations for Non-symmetric
- dndrv6
- Spectral Transformations for Non-symmetric
- zndrv1
- Standard Mode
- zndrv2
- Shift and Invert Spectral
- [s,d]seigt
- no title
- [s,d]Yconv
- no title
- Xneigh
- no title
- accuracy
- checking
- Postprocessing and Accuracy Checking
| Postprocessing and Accuracy Checking
| Post-processing and Accuracy Checking
| Accuracy checking
- Arnoldi
- block
- Block Methods
- compressed factorization
- Implicit Restarting
- factorization
- The Arnoldi Factorization
- orthogonal vectors
- The Arnoldi Factorization
- relation
- The Arnoldi Factorization
- vectors
- The Arnoldi Factorization
- ARPACK
- Introduction to ARPACK
- Amount of disk storage
- Installation
- Availability by ftp
- Availability
- Availability by URL
- Availability
- Availability in ScaLAPACK
- Availability
- Compliance with ANSI standard Fortran
- Expected Performance
- Contributions to
- Contributed Additions
- Expected performance
- Expected Performance
- installation
- Installation
- library
- Directory Structure and Contents
- makefile
- Installation
- Parallel
- P_ARPACK
- subroutines
- ARPACK subroutines
- availability
- Availability
- B-orthogonal
- Computational Routines
- backward error
- Stopping Criterion
- basis
- standard
- Structure of the Eigenvalue
- BLACS
- P_ARPACK
- BLAS
- Dependence on LAPACK and
| Computational Routines
- used by ARPACK
- BLAS routines used by
- blockArnoldi
- Block Methods
- bulge chases of QR
- Structure of the Eigenvalue
- characteristic polynomial
- Structure of the Eigenvalue
- Chebyshev
- polynomial
- XYaup2
- check pointing
- Tracking the progress of
| Check Pointing ARPACK
- choice of shifts
- Implicit Restarting
- exact ones
- Implicit Restarting
- Cholesky factorization of
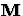
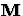 is Hermitian Positive
is Hermitian Positive
- classical Gram-Schmidt
- XYaitr
- complex
- Hermitian
- Band Drivers
- computing eigenvectors
- dseupd
- Post-Processing for Eigenvectors Using dseupd
- dneupd
- Post-Processing for Eigenvectors Using dneupd
- zneupd
- Post-Processing for Eigenvectors Using zneupd
- computing interior eigenvalues
- Using the Computational Modes
- computing Schur vectors
- dneupd
- Post-Processing for Eigenvectors Using dneupd
- zneupd
- Post-Processing for Eigenvectors Using zneupd
- condition number
- 2-norm condition estimator
- The SVD Drivers
- of a matrix
- The SVD Drivers
- Contents of ARPACK
- Directory Structure and Contents
- contribution
- Contributed Additions
- Contributions to ARPACK
- Contributed Additions
- convention
- naming
- ARPACK subroutines
- convergence of IRAM
- XYaup2
- convex hull
- Shift and Invert Spectral
- cost
- computational
- Computational Routines
- of implicit restart
- Using the Computational Modes
- data
- type
- Naming Conventions, Precisions and
| ARPACK subroutines
- data structure
- Identify OP and B
- Data types
- Naming Conventions, Precisions and
- debugging
- Tracking the progress of
- Debugging capability
- Trace Debugging Capability
- defective
- Structure of the Eigenvalue
- deflation
- Implicit Restarting
- departure from normality
- Stopping Criterion
- DGKS
- The Arnoldi Factorization
- correction
- The Arnoldi Factorization
| XYaitr
- direct methods
- factoring shift-invert
- Shift and Invert Spectral
- direct residual
- Stopping Criterion
- directories of ARPACK
- ARMAKES
- Directory Structure and Contents
- BAND
- Directory Structure and Contents
- BLAS
- Directory Structure and Contents
- COMPLEX
- Directory Structure and Contents
- DOCUMENTS
- Directory Structure and Contents
- EXAMPLES
- Directory Structure and Contents
- LAPACK
- Directory Structure and Contents
- NONSYM
- Directory Structure and Contents
- SRC
- Directory Structure and Contents
- SVD
- Directory Structure and Contents
- SYM
- Directory Structure and Contents
- UTIL
- Directory Structure and Contents
- dominant eigenvalue
- Structure of the Eigenvalue
- driver routines
- example
- Templates and Driver Routines
- simple
- Getting Started
- drivers
- band
- Band Drivers
- complex
- Complex Drivers
- non-symmetric
- Real Nonsymmetric Drivers
- selection
- Selecting a Symmetric Driver
- SVD
- The SVD Drivers
- symmetric
- Symmetric Drivers
- eigenpair
- Structure of the Eigenvalue
- eigenvalue problems
- generalized
- Generalized Eigenvalue Problem
| Generalized Nonsymmetric Eigenvalue Problem
| Generalized Eigenvalue Problems
- standard
- Setting up the problem
- eigenvalues
- Structure of the Eigenvalue
- accuracy
- Stopping Criterion
- clustered
- Shift and Invert Spectral
- conjugate pair
- Post-Processing for Eigenvectors Using dneupd
- distinct
- Structure of the Eigenvalue
- dominant
- Structure of the Eigenvalue
- extremal
- Shift and Invert Spectral
- infinite
- Shift and Invert Spectral
| Structure of the Spectral
- interior
- Shift and Invert Spectral
- largest
- imaginary part
- Standard Mode
- magnitude
- Standard Mode
- real part
- Standard Mode
- largest
- largest
- multiple
- Stopping Criterion
| The Arnoldi Factorization
| Block Methods
| Other Variables
| Other Variables
| Other Variables
| Modify other variables if
- non-clustered
- Shift and Invert Spectral
- sensitivity
- Stopping Criterion
- smallest
- magnitude
- Standard Mode
- imaginary part
- Standard Mode
- real part
- Standard Mode
- smallest
- smallest
- spurious
- The Arnoldi Factorization
- wanted
- Implicit Restarting
- well separated
- Shift and Invert Spectral
- eigenvector
- Structure of the Eigenvalue
- accuracy
- Stopping Criterion
- left
- Structure of the Eigenvalue
- normalization
- Post Processing for Eigenvalues
| Post-Processing for Eigenvectors Using dseupd
| Post-Processing for Eigenvectors Using dneupd
| Post-Processing for Eigenvectors Using zneupd
| XYeupd
- purification
- Post-Processing for Eigenvectors Using dseupd
| Post-Processing for Eigenvectors Using dneupd
| Post-Processing for Eigenvectors Using zneupd
- right
- Structure of the Eigenvalue
| Krylov Subspaces and Projection
- sensitivity
- Stopping Criterion
- simple
- Structure of the Eigenvalue
- eigenvectors
- complex eigenvectors in real arithmetic
- Post-Processing for Eigenvectors Using dneupd
- purification
- Eigenvector/Null-Space Purification
- error
- backward
- Stopping Criterion
- residual
- Eigenvector/Null-Space Purification
- exact shifts
- Implicit Restarting
- example driver for using dsaupd
- An Example for a
- execution
- rate of
- Computational Routines
- extremal eigenvalues
- Shift and Invert Spectral
- filter
- Implicit Restarting
- Fortran77
- Introduction to ARPACK
- Galerkin condition
- Krylov Subspaces and Projection
- GMRES
- The Arnoldi Factorization
- Hessenberg decomposition
- The Arnoldi Factorization
- Hessenberg matrix
- Structure of the Eigenvalue
- ill-conditioned
- Shift and Invert Spectral
- mass matrix
- The Generalized Eigenvalue Problem
- implicit restart
- Implicit Restarting
- implicit shifts
- exact
- Initial Parameter Settings
- Improving convergence
- with spectral transformations
- Shift and Invert Spectral
- include
- Obtaining Trace Output
- include files
- Expected Performance
- indefinite linear systems
- Shift and Invert Spectral
- Initial parameter settings
- for dsaupd
- Initial Parameter Settings
- initial vector
- generating of
- Xgetv0
- inner product
- Shift and Invert Spectral
| The Generalized Eigenvalue Problem
- weighted
- Shift and Invert Spectral
- invariant subspace
- Structure of the Eigenvalue
- sensitivity
- Structure of the Eigenvalue
| Stopping Criterion
- IRAM
- Introduction to ARPACK
| The Implicitly Restarted Arnoldi
- convergence rate
- XYaup2
- IRLM
- Introduction to ARPACK
- Iterative methods
- shift-invert
- Shift and Invert Spectral
- Krylov
- Krylov Subspaces and Projection
- block subspace
- Block Methods
- invariant subspace
- Krylov Subspaces and Projection
- projection methods
- Krylov Subspaces and Projection
- subspace
- Krylov Subspaces and Projection
- Krylov methods
- link with power method
- Krylov Subspaces and Projection
- Lanczos
- Introduction to ARPACK
- block method
- Eigenvector/Null-Space Purification
- factorization
- The Arnoldi Factorization
- orthogonal vectors
- The Arnoldi Factorization
- vectors
- The Arnoldi Factorization
- LAPACK
- Dependence on LAPACK and
| Computational Routines
- used by ARPACK
- LAPACK routines used by
- loss of orthogonality
- The Arnoldi Factorization
- M-Arnoldi process
- Structure of the Spectral
| Structure of the Spectral
- M-inner product
- Shift and Invert Spectral
| Cayley Transformation Mode
- machine precision
- Stopping Criterion
| Shift and Invert Spectral
| Stopping Criterion
| [s,d]Yconv
- matrix
- Hessenberg
- Structure of the Eigenvalue
- Jordan form
- Structure of the Eigenvalue
- mass
- The Generalized Eigenvalue Problem
- normal
- Structure of the Eigenvalue
- overlap
- The Generalized Eigenvalue Problem
- Schur form
- Structure of the Eigenvalue
- stiffness
- The Generalized Eigenvalue Problem
| The Generalized Eigenvalue Problem
- tridiagonal
- Structure of the Eigenvalue
- matrix factorization
- direct
- Getting Started with ARPACK
- message passing
- P_ARPACK
- mode
- Buckling
- Buckling Mode
- Cayley
- Cayley Transformation Mode
- regular-inverse
- Regular Inverse Mode
| Regular Inverse Mode
| Regular Inverse Mode
- shift-invert
- Shift-Invert Mode
| General Shift-Invert Spectral Transformation
- standard
- Standard Mode
- modes, computational
- Buckling
- Using the Computational Modes
- Cayley
- Using the Computational Modes
- complex
- Computational Modes for Complex
- non-symmetric
- Computational Modes for Real
- regular
- Using the Computational Modes
- regular-inverse
- Using the Computational Modes
- shift-invert
- Using the Computational Modes
- symmetric
- Computational Modes for Real
- MPI
- P_ARPACK
- multiplicity
- algebraic
- Structure of the Eigenvalue
- geometric
- Structure of the Eigenvalue
- missed
- Stopping Criterion
| Other Variables
| Other Variables
| Other Variables
| Modify other variables if
- Naming conventions
- Naming Conventions, Precisions and
- Netlib
- Availability
- non-clustered eigenvalues
- Shift and Invert Spectral
- notation
- Structure of the Eigenvalue
- orthogonality
- Arnoldi vectors
- The Arnoldi Factorization
- Lanczos vectors
- The Arnoldi Factorization
- parallel ARPACK
- P_ARPACK
- polynomial
- acceleration
- Implicit Restarting
- characteristic
- Structure of the Eigenvalue
- Chebyshev
- XYaup2
- filter
- Implicit Restarting
- implicitly applied
- Implicit Restarting
- polynomial restarting
- Implicit Restarting
- post-processing
- Postprocessing and Accuracy Checking
| Postprocessing and Accuracy Checking
| Post-processing and Accuracy Checking
- power method
- Structure of the Eigenvalue
- precision
- Naming Conventions, Precisions and
- Precision of data
- Naming Conventions, Precisions and
- Problems with ARPACK
- Trouble Shooting and Problems
- projection methods
- Krylov
- Krylov Subspaces and Projection
- purging
- Implicit Restarting
- purification of eigenvectors
- Eigenvector/Null-Space Purification
- QR
- algorithm
- Structure of the Eigenvalue
- as subspace iteration
- Implicit Restarting
- factorization
- Structure of the Eigenvalue
- iteration
- Structure of the Eigenvalue
| XYapps
- truncated iteration
- Implicit Restarting
| Implicit Restarting
- range
- Xgetv0
- Rayleigh quotient
- The Arnoldi Factorization
- residual
- The Arnoldi Factorization
- README
- Availability
- Research Funding of ARPACK
- Research Funding of ARPACK
- restarting
- Implicit Restarting
- exact shifts
- Implicit Restarting
- filtering
- Implicit Restarting
- implicitly
- Implicit Restarting
- polynomial
- Implicit Restarting
- reverse communication
- Important Features
| Reverse Communication Interface
| The Reverse Communication Interface
| The Reverse Communication Interface
- flag
- Initial Parameter Settings
- shift-invert transformation
- Reverse Communication Structure for
- Ritz
- estimate
- The Arnoldi Factorization
- value
- Krylov Subspaces and Projection
- vector
- Krylov Subspaces and Projection
- routines
- computational
- Computational Routines
- Schur decomposition
- Structure of the Eigenvalue
- partial
- Structure of the Eigenvalue
| Krylov Subspaces and Projection
- self-adjoint
- The Generalized Eigenvalue Problem
- semi-inner product
- Shift and Invert Spectral
- sep
- Stopping Criterion
- Setting nev and ncv
- Using the Computational Modes
- Setting nev and ncv
- Setting up the problem
- shift-invert
- Shift and Invert Spectral
- shifts
- exact
- Implicit Restarting
- implicit
- ARPACK subroutines
- similar
- Structure of the Eigenvalue
- similarity transformation
- Structure of the Eigenvalue
- SIMPLE
- Directory Structure and Contents
- simple driver
- symmetric eigenvalue problem
- An Example for a
- simple driver dssimp
- An Example for a
- singular
- Shift and Invert Spectral
- singular mass matrix
- Structure of the Spectral
- singular value decomposition
- The Singular Value Decomposition
- singular vectors
- left
- The Singular Value Decomposition
- right
- The Singular Value Decomposition
- spectral enhancement
- Shift and Invert Spectral
- spectral transformation
- Shift and Invert Spectral
| Structure of the Spectral
| Spectral Transformations for Non-symmetric
- deciding
- Shift and Invert Spectral
- enhance convergence
- Structure of the Spectral
- factorization with a direct method
- Shift and Invert Spectral
- linear systems
- Shift and Invert Spectral
- matrix factorization
- Shift and Invert Spectral
- spectrum
- Structure of the Eigenvalue
- standard eigenvalue problem
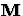 is Hermitian Positive
is Hermitian Positive
- starting vector
- Setting the Starting Vector
- stopping criterion
- Stopping Criterion
- Ritz estimate
- Stopping Criterion
- symmetric eigenvalue problems
- Stopping Criterion
- subroutines of ARPACK
- auxiliary
- ARPACK subroutines
- subspace
- invariant
- Structure of the Eigenvalue
- subspace iteration
- Implicit Restarting
- as QR iteration
- Implicit Restarting
- SVD
- The Singular Value Decomposition
- templates
- simple
- Getting Started
- three term recurrence
- The Arnoldi Factorization
- tridiagonal matrix
- Structure of the Eigenvalue
- Trouble shooting ARPACK
- Trouble Shooting and Problems
- unitary
- matrix
- Structure of the Eigenvalue
- variable
- problem dependent
- Modify the Problem Dependent
- variables
- other
- Other Variables
| Other Variables
| Other Variables
| Modify other variables if
- problem dependent
- Modify the Problem Dependent
| Modify the Problem Dependent
| Modify problem dependent variables
- well separated eigenvalues
- Shift and Invert Spectral
Chao Yang
11/7/1997