



Next: is NOT Hermitian Positive
Up: Shift and Invert Spectral
Previous: Shift and Invert Spectral
If 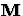 is Hermitian positive definite and well
conditioned ( is of modest size), then
computing the Cholesky factorization
and converting
equation (3.2.1) to
provides a transformation to a standard eigenvalue problem.
In this case, a request for a matrix vector product would be satisfied
with the following three steps:
is Hermitian positive definite and well
conditioned ( is of modest size), then
computing the Cholesky factorization
and converting
equation (3.2.1) to
provides a transformation to a standard eigenvalue problem.
In this case, a request for a matrix vector product would be satisfied
with the following three steps:
- 1.
- Solve for
- 2.
- Matrix-vector multiply
- 3.
- Solve for
Upon convergence, a computed eigenvector for is converted to an eigenvector of the original problem by
solving the the triangular system This transformation
is most appropriate when 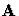 is Hermitian,
is Hermitian, 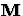 is Hermitian
positive definite and extremal eigenvalues are sought. This is
because will be Hermitian when
is Hermitian
positive definite and extremal eigenvalues are sought. This is
because will be Hermitian when 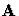 is.
is.
If 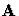 is Hermitian positive definite and the smallest eigenvalues are
sought, then it would be best to reverse the roles of
is Hermitian positive definite and the smallest eigenvalues are
sought, then it would be best to reverse the roles of 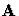 and
and 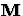 in the
above description and ask for the largest algebraic eigenvalues
or those of largest magnitude. Upon convergence,
a computed eigenvalue would
then be converted to an eigenvalue of the original
problem by the relation
in the
above description and ask for the largest algebraic eigenvalues
or those of largest magnitude. Upon convergence,
a computed eigenvalue would
then be converted to an eigenvalue of the original
problem by the relation




Next: is NOT Hermitian Positive
Up: Shift and Invert Spectral
Previous: Shift and Invert Spectral
Chao Yang
11/7/1997
![]() is Hermitian positive definite and the smallest eigenvalues are
sought, then it would be best to reverse the roles of
is Hermitian positive definite and the smallest eigenvalues are
sought, then it would be best to reverse the roles of ![]() and
and ![]() in the
above description and ask for the largest algebraic eigenvalues
or those of largest magnitude. Upon convergence,
a computed eigenvalue would
then be converted to an eigenvalue of the original
problem by the relation
in the
above description and ask for the largest algebraic eigenvalues
or those of largest magnitude. Upon convergence,
a computed eigenvalue would
then be converted to an eigenvalue of the original
problem by the relation