- (a)
- Solve in regular mode.
- (b)
- and
- (a)
- Solve in shift-invert mode.
- (b)
- and
- (a)
- Solve
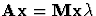 in regular inverse mode.
in regular inverse mode.
- (b)
- and
- (a)
- Solve
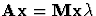 in shift-invert mode.
in shift-invert mode.
- (b)
- and
- (a)
- Solve in Buckling mode.
- (b)
- and
- (a)
- Solve
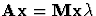 in Cayley mode.
in Cayley mode.
- (b)
- and
The reverse communication interface subroutine for symmetric eigenvalue problems is dsaupd . The subroutine is called as shown in Figure 3.4. The argument which may be any one of the settings listed in Table 3.3.
call dsaupd (ido, bmat, n, which, nev, tol, resid, ncv, v,
& ldv, iparam, ipntr, workd, workl, lworkl, info)
1|cWHICH
1c|DESCRIPTION
`LA'
Largest algebraic eigenvalues.
`SA'
Smallest algebraic eigenvalues.
`LM'
Eigenvalues largest in magnitude.
`SM'
Eigenvalues smallest in magnitude.
`BE'
Compute nev eigenvalues, half from
each end of the spectrum. When nev
is odd, compute one more from the
high end than from the low end.
The following is a list of the spectral transformation options for symmetric eigenvalue problems. In the following list, the specification of OP and are given for the various modes. Also, the iparam(7) and bmat settings are listed along with the name of the sample driver for the given mode. Sample drivers for the following modes may be found in the EXAMPLES/SYM subdirectory.