Naming Conventions, Precisions and Types

       ARPACK has two interface routines that must be invoked by the user. They are __aupd  that implements the IRAM and __eupd  to post process the results of __aupd. The user may request an orthogonal basis for a selected invariant subspace or eigenvectors corresponding to selected eigenvalues with __eupd. If a spectral transformation is used, __eupd transforms the computed eigenvalues for the problem

Both __aupd and __eupd are available for several combinations of problem type (symmetric and non-symmetric), data type (real, complex), and precision (single, double). The first letter (s,d,c,z) denotes precision  and data type.   The second letter denotes whether the problem is symmetric (s) or non-symmetric (n). Table 3.1 lists the possibilities.

 

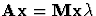
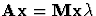
FIRST LETTER PRECISION DATA TYPE

s Single Real

d Double Real

c Single Complex

z Double Complex

 

1|cROUTINE 1c|DESCRIPTION

dsaupd Top level reverse communication interface to solve real double precision symmetric problems.

dseupd Post processing routine used to compute eigenvectors associated with the computed eigenvalues. This requires output from a converged application of dsaupd.

dnaupd Top level reverse communication interface to solve real double precision non-symmetric problems.

dneupd Post processing routine used to compute eigenvectors and/or Schur vectors corresponding to the invariant subspace associated with the computed eigenvalues. This requires output from a converged application of dnaupd.

znaupd Top level reverse communication interface to solve double precision complex arithmetic problems. This routine should be used for both Hermitian and Non-Hermitian problems.

zneupd Post processing routine used to compute eigenvectors and/or Schur vectors corresponding to the invariant subspace associated with the computed eigenvalues in complex arithmetic. This requires output from a converged application of znaupd.

Thus, dnaupd is the routine to use if the problem is a double precision nonsymmetric (standard or generalized) problem and dneupd is the post-processing routine to use in conjunction with dnaupd to recover eigenvalues and eigenvectors of the original problem upon convergence. For complex matrices, one should use _naupd and _neupd with the first letter either c or z regardless of whether the problem is Hermitian or non-Hermitian. Table 3.2 lists the double precision routines available.