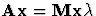
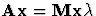
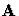 and
and 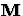 are real or complex
are real or complex 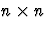 matrices.
matrices.
The shift and invert spectral transformation is used to enhance
convergence to a desired portion of the spectrum.
If (x,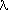 ) is an eigenpair for
) is an eigenpair for
(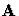 ,
,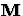 ) and
) and 
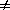
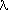 then
then
(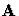 -
- 
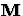 )
-1
)
-1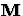 x = x
x = x , where
, where
 = 1/(
= 1/(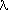 -
-  )
)
 since the nev eigenvalues
since the nev eigenvalues  j of that are largest in
magnitude correspond to the nev eigenvalues
j of that are largest in
magnitude correspond to the nev eigenvalues 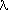 j of
the original problem that are nearest to the shift
j of
the original problem that are nearest to the shift  in
absolute value. These transformed eigenvalues of largest magnitude
are precisely the eigenvalues that are easy to compute with a Krylov method.
Once they are found, they may be transformed back to eigenvalues
of the original problem. The direct relation is
in
absolute value. These transformed eigenvalues of largest magnitude
are precisely the eigenvalues that are easy to compute with a Krylov method.
Once they are found, they may be transformed back to eigenvalues
of the original problem. The direct relation is
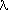 j =
j =  +
1/
+
1/ j,
j,
In general, will be non-Hermitian even if ![]() and
and ![]() are both
Hermitian. However, this is easily remedied. The assumption that
are both
Hermitian. However, this is easily remedied. The assumption that ![]() is
Hermitian positive definite implies that the bi-linear form
is
Hermitian positive definite implies that the bi-linear form
Shift-invert spectral transformations are very effective and should even be used on standard problems () whenever possible. This is particularly true when interior eigenvalues are sought or when the desired eigenvalues are clustered. Roughly speaking, a set of eigenvalues is clustered if the maximum distance between any two eigenvalues in that set is much smaller than the maximum distance between any two eigenvalues of .
If one has a generalized
problem (), then one must provide a way
to solve linear systems
with either ![]() ,
, ![]() or a linear combination of the two matrices
in order to use ARPACK.
In this case, a sparse direct method should be used to factor
the appropriate matrix whenever possible.
The resulting factorization may be used repeatedly to solve the
required linear systems once it has been obtained.
If an iterative method is used for the linear
system
solves, the accuracy of the solutions must be commensurate with the
convergence tolerance used for ARPACK. A slightly
more stringent tolerance is needed for the iterative linear
system solves (relative to the desired accuracy of the eigenvalue
calculation).
See [18,32,30,40] for further information and
references.
or a linear combination of the two matrices
in order to use ARPACK.
In this case, a sparse direct method should be used to factor
the appropriate matrix whenever possible.
The resulting factorization may be used repeatedly to solve the
required linear systems once it has been obtained.
If an iterative method is used for the linear
system
solves, the accuracy of the solutions must be commensurate with the
convergence tolerance used for ARPACK. A slightly
more stringent tolerance is needed for the iterative linear
system solves (relative to the desired accuracy of the eigenvalue
calculation).
See [18,32,30,40] for further information and
references.
The main drawback with using the shift-invert spectral transformation is that the coefficient matrix is typically indefinite in the Hermitian case and has in the interior of the convex hull of the spectrum in the non-Hermitian case. These are typically the most difficult situations for iterative methods and also for sparse direct methods.
The decision to use a spectral transformation on a standard
eigenvalue problem () or to use one of the simple modes
described in Chapter 2 is problem dependent. The simple
modes have the advantage that one only need supply a
matrix vector product ![]() . However, this approach is
usually only successful for problems where extremal non-clustered
eigenvalues are sought. In non-Hermitian problems, extremal means
eigenvalues near the boundary
of the convex hull of the spectrum of
. However, this approach is
usually only successful for problems where extremal non-clustered
eigenvalues are sought. In non-Hermitian problems, extremal means
eigenvalues near the boundary
of the convex hull of the spectrum of ![]() .
For Hermitian problems, extremal means
eigenvalues at the left or right end points of the spectrum of
.
For Hermitian problems, extremal means
eigenvalues at the left or right end points of the spectrum of ![]() .
The notion of non-clustered (or well separated)
is difficult to
define without going into considerable detail. A simplistic notion
of a well-separated eigenvalue for a Hermitian problem would
be
for all with
Unless a matrix vector
product is quite difficult to code or extremely expensive computationally,
it is probably worth trying to use the simple mode first if you are
seeking extremal eigenvalues.
.
The notion of non-clustered (or well separated)
is difficult to
define without going into considerable detail. A simplistic notion
of a well-separated eigenvalue for a Hermitian problem would
be
for all with
Unless a matrix vector
product is quite difficult to code or extremely expensive computationally,
it is probably worth trying to use the simple mode first if you are
seeking extremal eigenvalues.
The remainder of this section discusses additional transformations
that may be applied to convert a generalized eigenproblem to a
standard eigenproblem. These are appropriate when ![]() is
well conditioned (Hermitian or non-Hermitian).
is
well conditioned (Hermitian or non-Hermitian).