Definition : If then a relation of the form
where has orthonormal columns, and is upper Hessenberg with non-negative subdiagonal elements is called a k-step Arnoldi Factorization of IfThe preceding development of this factorization has been purely through the consequences of the orthogonal projection imposed by the Galerkin conditions. (A more straightforward but less illuminating derivation is to equate the first k columns of the Hessenberg decomposition )An alternative way to write this factorization is
This factorization may be used to obtain approximate solutions to a linear system if and this underlies the GMRES method [41]. However, the purpose here is to investigate the use of this factorization to obtain approximate eigenvalues and eigenvectors. The discussion of the previous section implies that Ritz pairs satisfying the Galerkin condition are immediately available from the eigenpairs of the small projected matrix
If then the vector satisfies
The number is called the Ritz estimate for the the Ritz pair as an approximate eigenpair for Observe that if is a Ritz pair then is a Rayleigh quotient (assuming ) and the associated Rayleigh quotient residual satisfies When
The k-step factorization
may be advanced one step at the cost of a (sparse) matrix-vector product
involving ![]() and two dense matrix vector products involving
and The explicit steps needed to form a k-Step Arnoldi
factorization are
listed in Algorithm 2 shown in Figure 4.3.
In exact arithmetic, the columns of form an orthonormal basis for the
Krylov subspace and is the orthogonal projection of
and two dense matrix vector products involving
and The explicit steps needed to form a k-Step Arnoldi
factorization are
listed in Algorithm 2 shown in Figure 4.3.
In exact arithmetic, the columns of form an orthonormal basis for the
Krylov subspace and is the orthogonal projection of ![]() onto this
space.
In finite precision arithmetic, care must be taken to assure that the
computed vectors are orthogonal to working precision. The method
proposed by Daniel, Gragg, Kaufman and Stewart (DGKS)
in [9] provides an excellent way to construct
a vector that
is numerically orthogonal to . It amounts to computing a
correction
onto this
space.
In finite precision arithmetic, care must be taken to assure that the
computed vectors are orthogonal to working precision. The method
proposed by Daniel, Gragg, Kaufman and Stewart (DGKS)
in [9] provides an excellent way to construct
a vector that
is numerically orthogonal to . It amounts to computing a
correction
Put
Put
(a2.3)
Input: (
![]() )
)
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
For
![]() ,
,
(a2.1)
End_For
![]() ;
;
![]() ;
;
(a2.2)
![]() ;
;
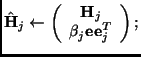
![]() ;
;
(a2.4)
![]()
![]()
(a2.5)
![]()
The dense matrix-vector products at Step (a2.4) and also the correction
may be accomplished using
Level 2 BLAS. This is important for performance on vector,
and parallel-vector supercomputers. The Level 2 BLAS operation _GEMV is easily
parallelized and vectorized and has a much better ratio of floating
point computation to data movement [11,12] than the
Level 1 BLAS operations.
The information obtained through this process is completely determined by the choice of the starting vector. Eigen-information of interest may not appear until k gets very large. In this case it becomes intractable to maintain numerical orthogonality of the basis vectors . Moreover, extensive storage will be required and repeatedly finding the eigensystem of will become prohibitive at a cost of flops.
Failure to maintain orthogonality leads to several numerical difficulties. In a certain sense, the computation (or approximation) of the projection indicated at Step (a2.4) in a way that overcomes these difficulties has been the main source of research activity for the Lanczos method. Paige [35] showed that the loss of orthogonality occurs precisely when an eigenvalue of is close to an eigenvalue of In fact, the Lanczos vectors lose orthogonality in the direction of the associated approximate eigenvector. Moreover, failure to maintain orthogonality results in spurious copies of the approximate eigenvalue produced by the Lanczos method. Implementations based on selective and partial orthogonalization [18,38,43] monitor the loss of orthogonality and perform additional orthogonalization steps only when necessary. The approaches given in [8,7,37] use only the three term recurrence with no additional orthogonalization steps. These strategies determine whether multiple eigenvalues produced by the Lanczos method are spurious or correspond to true multiple eigenvalue of However, these approaches do not generate eigenvectors directly. Additional computation is required if eigenvectors are needed and this amounts to re-generating the basis vectors with the Lanczos process.
A related numerical difficulty associated with failure to maintain orthogonality stems from the fact that if and only if the columns of span an invariant subspace of When ``nearly'' spans such a subspace, should be small. Typically, in this situation, a loss of significant digits will take place at Step (a2.4) through numerical cancellation unless special care is taken (i.e. use of the DGKS correction).
Understanding this difficulty and overcoming it is essential for the IRA iteration which is designed to drive to . It is desirable for to become small because this indicates that the eigenvalues of are the eigenvalues of a slightly perturbed matrix that is near to This is easily seen from a re-arrangement of the Arnoldi relation:
where . Hence, is an invariant subspace for the perturbed matrix with Thus, the eigenvalues of will be accurate approximations to the eigenvalues of