



Next: Reverse Communication Structure for
Up: Shift and Invert Spectral
Previous: is Hermitian Positive Definite
If neither 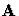 nor
nor 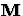 is Hermitian positive semi-definite, then
a direct transformation to standard form is required.
One simple way to obtain a direct transformation of
equation (3.2.1) to a standard
eigenvalue problem is to multiply on
the left by which results in
Of course, one should not perform this
transformation explicitly since it will most likely convert a
sparse problem into a dense one. If possible, one should obtain
a direct factorization of
is Hermitian positive semi-definite, then
a direct transformation to standard form is required.
One simple way to obtain a direct transformation of
equation (3.2.1) to a standard
eigenvalue problem is to multiply on
the left by which results in
Of course, one should not perform this
transformation explicitly since it will most likely convert a
sparse problem into a dense one. If possible, one should obtain
a direct factorization of 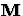 and when a matrix-vector product
involving is called for, it may be accomplished with the following
two steps:
and when a matrix-vector product
involving is called for, it may be accomplished with the following
two steps:
- 1.
- Matrix-vector multiply
- 2.
- Solve:
Several problem dependent issues may modify this strategy. If 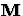 is singular or if one is interested in eigenvalues near a point then a user may choose to work with but without using the
is singular or if one is interested in eigenvalues near a point then a user may choose to work with but without using the 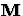 -inner products discussed previously.
In this case the user will have to transform the converged
eigenvalues of to eigenvalues of the
original problem.
-inner products discussed previously.
In this case the user will have to transform the converged
eigenvalues of to eigenvalues of the
original problem.




Next: Reverse Communication Structure for
Up: Shift and Invert Spectral
Previous: is Hermitian Positive Definite
Chao Yang
11/7/1997
![]() is singular or if one is interested in eigenvalues near a point then a user may choose to work with but without using the
is singular or if one is interested in eigenvalues near a point then a user may choose to work with but without using the ![]() -inner products discussed previously.
In this case the user will have to transform the converged
eigenvalues of to eigenvalues of the
original problem.
-inner products discussed previously.
In this case the user will have to transform the converged
eigenvalues of to eigenvalues of the
original problem.