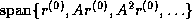 . In GMRES, this
basis is formed explicitly:
. In GMRES, this
basis is formed explicitly:




The Generalized Minimal Residual method [189] is an extension of MINRES (which is only applicable to symmetric systems) to unsymmetric systems. Like MINRES, it generates a sequence of orthogonal vectors, but in the absence of symmetry this can no longer be done with short recurrences; instead, all previously computed vectors in the orthogonal sequence have to be retained. For this reason, ``restarted '' versions of the method are used.
In the Conjugate Gradient method, the residuals form an orthogonal
basis
for the space 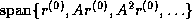 . In GMRES, this
basis is formed explicitly:
. In GMRES, this
basis is formed explicitly:
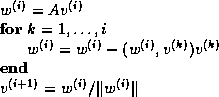
The reader may recognize this as a modified Gram-Schmidt
orthogonalization.
Applied to the Krylov
sequence
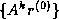 this orthogonalization
is called the ``Arnoldi method'' [6].
The inner product coefficients
this orthogonalization
is called the ``Arnoldi method'' [6].
The inner product coefficients 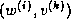 and
and
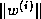 are stored in an upper Hessenberg matrix.
are stored in an upper Hessenberg matrix.
The GMRES iterates are constructed as
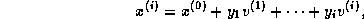
where the coefficients 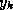 have been chosen to minimize the residual
norm
have been chosen to minimize the residual
norm 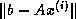 . The GMRES algorithm has the property that this
residual norm can be computed without the iterate having been formed.
Thus, the expensive action of forming the iterate can be postponed
until the residual norm is deemed small enough.
. The GMRES algorithm has the property that this
residual norm can be computed without the iterate having been formed.
Thus, the expensive action of forming the iterate can be postponed
until the residual norm is deemed small enough.
The pseudocode for the restarted
GMRES(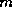 ) algorithm with preconditioner
) algorithm with preconditioner 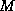 is given in
Figure
is given in
Figure  .
.

Figure: The Preconditioned GMRES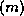 Method
Method