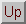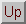



In recent years, much attention has been given to domain decomposition methods for linear elliptic problems that are based on a partitioning of the domain of the physical problem. Since the subdomains can be handled independently, such methods are very attractive for coarse-grain parallel computers. On the other hand, it should be stressed that they can be very effective even on sequential computers.
In this brief survey, we shall restrict ourselves to the standard second order self-adjoint scalar elliptic problems in two dimensions of the form:
where 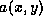 is a positive function on the domain
is a positive function on the domain 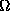 , on whose
boundary the value of
, on whose
boundary the value of  is prescribed (the Dirichlet problem). For
more general problems, and a good set of references, the reader is
referred to the series of
proceedings [177][135][107][49][48][47]
and the surveys [196][51].
is prescribed (the Dirichlet problem). For
more general problems, and a good set of references, the reader is
referred to the series of
proceedings [177][135][107][49][48][47]
and the surveys [196][51].
For the discretization of (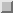 ), we shall assume for
simplicity that
), we shall assume for
simplicity that 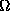 is triangulated by a set
is triangulated by a set 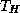 of nonoverlapping
coarse triangles (subdomains)
of nonoverlapping
coarse triangles (subdomains) 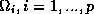 with
with 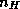 internal
vertices. The
internal
vertices. The 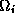 's are in turn
further refined into a set of smaller triangles
's are in turn
further refined into a set of smaller triangles 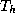 with
with  internal vertices in total.
Here
internal vertices in total.
Here 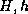 denote the coarse and fine mesh size respectively.
By a standard Ritz-Galerkin method using piecewise linear triangular
basis elements on (
denote the coarse and fine mesh size respectively.
By a standard Ritz-Galerkin method using piecewise linear triangular
basis elements on (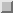 ), we obtain an
), we obtain an 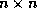 symmetric positive definite linear system
symmetric positive definite linear system
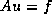 .
.
Generally, there are two kinds of approaches depending on whether the subdomains overlap with one another (Schwarz methods ) or are separated from one another by interfaces (Schur Complement methods , iterative substructuring).
We shall present domain decomposition methods as preconditioners
for the linear system 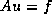 to
a reduced (Schur Complement) system
to
a reduced (Schur Complement) system
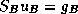 defined on the interfaces in the non-overlapping formulation.
When used with the standard Krylov subspace methods discussed
elsewhere in this book, the user has to supply a procedure
for computing
defined on the interfaces in the non-overlapping formulation.
When used with the standard Krylov subspace methods discussed
elsewhere in this book, the user has to supply a procedure
for computing 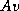 or
or 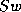 given
given  or
or 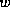 and the algorithms to be described
herein computes
and the algorithms to be described
herein computes 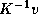 .
The computation of
.
The computation of 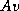 is a simple sparse matrix-vector
multiply, but
is a simple sparse matrix-vector
multiply, but 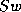 may require subdomain solves, as will be described later.
may require subdomain solves, as will be described later.