В заключение рассмотрим пример программы, в которой Aztec используется для решения системы уравнений, возникающей при конечно-разностной аппроксимации 3-х мерного оператора Лапласа. Для простоты мы не будем использовать систему уравнений, связанную с решением какой-либо реальной физической задачи, а вместо этого будем формировать правую часть таким образом, чтобы получить заранее известное решение, например,
X(i) = i + 1.

    program Aztec
c Параметры:
c ndim - максимальное число неизвестных,
c lda  - максимальный размер матрицы
    parameter (ndim = 125000, lda = 7*ndim)
    include 'mpif.h'
    include 'az_aztecf.h'
    integer n, nz
c
    integer i, ierror, recb(0:63), disp(0:63)
    double precision b(0:ndim), x(0:ndim), tmp(0:ndim)
    double precision s, time, total
c
    integer IAM, NPROCS
    integer N_update
    integer proc_config(0:AZ_PROC_SIZE), options(0:AZ_OPTIONS_SIZE)
    integer update(0:ndim), external(0:ndim), data_org(0:ndim)
    integer update_index(0:ndim), extern_index(0:ndim)
    integer bindx(0:lda)
    double precision params(0:AZ_PARAMS_SIZE)
    double precision status(0:AZ_STATUS_SIZE)
    double precision val(0:lda)
    common /global/ n
c Инициализация MPI (для Aztec не обязательна, если не использовать
c MPI функции)
    CALL MPI_Init(ierror)
c Получаем номер процессора и общее число процессоров,
c выделенных задаче
    call AZ_processor_info(proc_config)
    IAM = proc_config(AZ_node)
    NPROCS = proc_config (AZ_N_procs)
c
c На 0-м процессоре печатаем пояснительную информацию и считываем
c параметр, определяющий размер решаемой задачи
c (максимально 50х50х50)
    if (IAM.eq.0) then
    write(6,2)
 2  format(' '/
 $ ' Aztec example driver'//
 $ ' This program creates an MSR matrix corresponding to'/
 $ ' a 7pt discrete approximation to the 3D Poisson operator'/
 $ ' on an n x n x n square and solves it by various methods.'/
 $ ' n must be <= 50.'//)
    write (6,*) 'input number grid point on each direction n = '
    read(*,*) n
    endif
c Рассылаем считанный параметр всем процессорам
    call MPI_BCAST(n, 1, MPI_INTEGER, 0, MPI_COMM_WORLD, ierr)
c Вычисляем количество неизвестных в системе
    nz = n*n*n

c Цикл по всем методам решения
    DO 777 K = 0,4
    time = MPI_Wtime()
c Определяем параметры разбиения матрицы по процессорам
    call AZ_read_update(N_update, update, proc_config, nz, 1, 0)
c Формируем матрицу в виде массивов val и bindx,
c в bindx(0) заносим номер позиции, с которой начнут располагаться
c недиагональные элементы, и выполняем цикл по всем строкам
    bindx(0) = N_update+1
    do 250 i = 0, N_update-1
      call add_row_7pt(update(i), i, val, bindx)
  250 continue
c Формируем правую часть системы таким образом, чтобы получить
c известное решениеа b(i) = 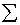A(i,j)*j
c
    do 341 i = 0, N_update-1
    in = bindx(i)
    ik = bindx(i+1) - 1
    s = val(i)*(update(i)+1)
    do 342 j = in,ik
    s = s + val(j)*(bindx(j)+1)
 342 continue
     tmp(i) = s
 341 continue
c
c Преобразуем глобальную индексацию в локальную
    call AZ_transform(proc_config, external, bindx, val, update,
  $                   update_index, extern_index, data_org,
  $                   N_update, NULL,NULL,NULL,NULL, AZ_MSR_MATRIX)
c Устанавливаем параметры для решателя
    call AZ_defaults(options, params)
    options(AZ_solver) = K
    options(AZ_precond) = AZ_dom_decomp
    options(AZ_subdomain_solve) = AZ_ilu
    options(4) = 1
    options(AZ_output) = AZ_none
    options(AZ_max_iter) = 2000
    params(AZ_tol) = 1.d-10
c 0-й процессор печатает параметры решения задачи
    if (IAM.eq.0) then
    write(6,780)
    write (6,*) '        The solution of method is =',К
    write (6,*) '        Dimension matrices =',nz,
 $  '   NPROCS = ', NPROCS
    endif
c Преобразуем правую часть в соответствии с новой индексацией
    do 350 i = 0, N_update-1
    x(update_index(i)) = 0.0
    b(update_index(i)) = tmp(i)
 350 continue
c Решаем систему уравнений
    call AZ_solve(x,b, options, params, NULL,bindx,NULL,NULL,
 $                NULL, val, data_org, status, proc_config)
c Полученное решение возвращаем к исходной индексации
    DO 415 I = 0,N_update - 1
 415 tmp(i) = x(update_index(i))

c Выполняем сборку полученных частей решения в один вектор
c
    CALL MPI_ALLgather(N_update, 1, MPI_INTEGER, recb, 1,
 $                     MPI_INTEGER, MPI_COMM_WORLD, ierror)
    DISP(0) = 0
    DO 404 I = 1,NPROCS-1
 404 DISP(I) = DISP(I-1) + RECB(I-1)
    CALL MPI_ALLgatherv(tmp, N_update, MPI_DOUBLE_PRECISION, x, recb,
 $              disp, MPI_DOUBLE_PRECISION, MPI_COMM_WORLD, ierror)

c Печатаем первую и последнюю компоненты решения
    nz1 = nz-1
    if (IAM.eq.0) then
    do 348 i = 0,nz1,nz1
    s = x(i)
    write (6,956) i,s
 348 continue
 956 format (2x,'i=',I12,2x,'x(i)=',F18.8)
    endif
c
    time = MPI_Wtime() - time
c
    if(IAM.eq.0) write(*,435) time
 435  FORMAT(2x,'TIME CALCULATION (SEC.) = ',F12.4)
 777  continue
c
    CALL MPI_FINALIZE(IERROR)
    stop
    end

c Подпрограмма добавления очередной строки в массивы val и bindx
    subroutine add_row_7pt(row, location, val, bindx)
    integer row, location, bindx(0:*)
    double precision val(0:*)
    integer n3,n,k
    common /global/ n
c Входные параметры:
c row        - глобальный номер добавляемой строки
c location   - локальный номер строки в процессоре

c n3 - максимально возможный номер столбца
    n3 = n*n*n - 1
c Далее выполняется проверка: существует ли в трехмерной решетке
c ближайший сосед по каждому из направлений; если да, то
c соответствующий матричный элемент заносится и
c счетчик увеличивается на 1
    k = bindx(location)
    bindx(k) = row + 1
    if (bindx(k).le.n3) then
    val(k) = -1.
    k = k + 1
    endif
    bindx(k) = row - 1
    if (bindx(k) .ge. 0) then
    val(k) = -1.
    k = k + 1
    endif
    bindx(k) = row + n
    if (bindx(k).le.n3) then
    val(k) = -1.0
    k = k + 1
    endif
    bindx(k) = row - n
    if (bindx(k).ge. 0) then
    val(k) = -1.0
    k = k + 1
    endif
    bindx(k) = row + n*n
    if (bindx(k) .le. n3) then
    val(k) = -1.0
    k = k + 1
    endif
    bindx(k) = row - n*n
    if (bindx(k) .ge. 0) then
    val(k) = -1.0
    k = k + 1
    endif
c Занесение диагонального матричного элемента
    val(location) = 6.0
c Подготовка следующего шага: заносим номер позиции, с которой
c будут располагаться недиагональные элементы следующей строки
    bindx(location+1) = k
    return
    end