
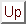


2.4. Хранение разреженных матриц в MSR формате
При использовании пакета Aztec самой сложной для программиста задачей является формирование надлежащим образом распределенной по процессорам матрицы.
На рис. 2.1 представлен пример разреженной матрицы 6x6. Предположим, что мы хотим распределить ее в 3 процессора (нумерация процессоров с 0). Если бы мы воспользовались процедурой AZ_read_update, то, скорее всего, для каждого процессора N_update было бы установлено равным 2, и в массив update были бы соответственно занесены значения (0,1), (2,3), (4,5).
Однако, для общности, рассмотрим другой вариант распределения. Пусть 0-й процессор хранит нулевую, первую и третью строки; 1-й процессор - одну четвертую строку; 2-й процессор - вторую и пятую строки. Этим самым мы однозначно задаем значения переменной N_update и массива update. Наша задача состоит в том, чтобы заполнить массивы bindx и val так, чтобы они адекватно описывали принятое распределение.
Массив val формируется следующим образом. Сначала в этот массив заносятся диагональные элементы хранимых строк, одна позиция пропускается (это сделано для соответствия с bindx) и затем, строка за строкой, в массив заносятся недиагональные ненулевые элементы (в том порядке, в котором они перечислены в массиве update).
В начале массива bindx хранятся номера позиций, с которых в массиве val начинаются недиагональные элементы соответствующей строки (включая и первую несуществующую - для того, чтобы можно было определить, сколько элементов в последней строке). Далее в массиве следуют номера столбцов, соответствующих ненулевым матричным элементам. Значения, которые должны быть занесены в соответствующие массивы в каждом процессоре, приведены ниже. Напоминаем, что индексация массивов начинается с 0.
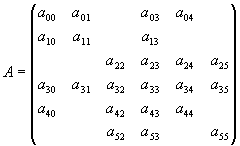
Рис. 2.1. Разреженная исходная матрица.
| proc0: | |||||||||||||||
| N_update: | 3 | ||||||||||||||
| update: | 0 | 1 | 3 | ||||||||||||
| index: | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | |
| bindx: | 4 | 7 | 9 | 14 | 1 | 3 | 4 | 0 | 3 | 0 | 1 | 2 | 4 | 5 | |
| val: | a00 | a11 | a33 | - | a01 | a03 | a04 | a10 | a13 | a30 | a31 | a32 | a34 | a35 | |
| _______________________________________________________________ | |||||||||||||||
| proc1: | ||||||
| N_update: | 1 | |||||
| update: | 4 | |||||
| index: | 0 | 1 | 2 | 3 | 4 | |
| bindx: | 2 | 5 | 0 | 2 | 3 | |
| val: | a44 | - | a40 | a42 | a43 | |
| ______________________________ | ||||||
| proc2: | |||||||||
| N_update: | 2 | ||||||||
| update: | 2 | 5 | |||||||
| index: | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| bindx: | 3 | 6 | 8 | 3 | 4 | 5 | 2 | 3 | |
| val: | a22 | a55 | - | a23 | a24 | a25 | a52 | a53 | |
| _________________________________________ | |||||||||
На практике, как было сказано выше, библиотека Aztec применяется для решения систем линейных алгебраических уравнений, возникающих при решении дифференциальных уравнений в частных производных. Для таких матриц, как правило, заранее известно количество ненулевых матричных элементов в строке и их местоположение в матрице, поэтому алгоритмы заполнения массивов val и bindx бывают достаточно простые.