![[DBPP]](pictures//asm_color_tiny.gif)





![[Search]](pictures//search_motif.gif)
Next: Chapter Notes
Up: 4 Putting Components Together
Previous: 4.7 Summary
-
Discuss ways in which modular design techniques are used in the design
of an automobile engine, house, or suspension bridge.
-
Identify ways in which modularity ideas might apply to the management
of an orchestra, educational institution, or company.
-
Develop analytic models for the maximum throughput (in requests
processed per second) supported by the centralized and distributed
tuple space implementations outlined in Section 4.5.
-
Using a language that supports concurrent composition, such as CC++
\
or Fortran M, implement centralized and distributed tuple space
modules. Study the performance of these modules in a simple parameter
study problem, and relate performance to the models of
Exercise 3.
-
Discuss ways in which the database search algorithm of
Section 4.5 could be modified to avoid the central
bottleneck inherent in a single manager.
-
An alternative parallel algorithm for the 2-D FFT considered in
Section 4.4.1 assumes a fixed 2-D decomposition of data
structures; hence, communication is required within each 1-D FFT. Use
a performance model to contrast this algorithm with those described in
the text. Assume that the communication costs for a 1-D FFT algorithm
operating on N
points on P
processors are
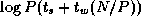 .
.
-
A problem comprises two components, A
and B
. A
can
be solved in 1000 seconds on computer C1
and in 5000 seconds on
computer C2
; B
requires 4000 and 2000 seconds on
C1
and C2
, respectively. The two computers are connected by a
1000-km optical fiber link that can transfer data at 100 MB/sec with a
latency of 10 msec. The two components can execute concurrently but
must transfer 10 MB of data 10,000 times during execution. Is it
cheapest (in terms of computational resources consumed) to solve the
problem on computer C1
, on computer
C2
, or on both computers together?
-
A problem similar to that of Exercise 7 is found to use fewer
computational resources when run on the two networked computers than
on either computer alone. Your public relations office
proposes to promote this as an example of superlinear speedup. Do you
agree?
-
A climate model consists of an atmosphere and ocean model. At each
step, the models both perform a finite difference computation and
exchange five 2-D arrays. Develop performance models for two
alternative parallel implementations, based on sequential and parallel
composition respectively. Discuss the relative performance of the two
implementations.
-
Determine the problem size and processor count regimes in which each
of the three convolution algorithms described in
Example 4.4 would be faster, assuming machine parameters
characteristic of (a) a multicomputer and (b) an Ethernet-connected
LAN.
-
The performance analysis of the pipelined algorithms considered in
Section 4.4 did not take into account idle time incurred
when starting up and shutting down pipelines. Refine the performance
models to account for these costs. How many images must be processed
before efficiency reaches 95 percent of that predicted in the absence
of these costs?
-
Execute by hand for N=P=4
the matrix multiplication algorithm
based on a 2-D decomposition described in Section 4.6.1.
-
A simpler variant of the multiplication algorithm for matrices
decomposed in two dimensions uses a ring rather than a tree for the
broadcast operations. Use performance models to compare the two
algorithm variants. (Note that a broadcast can be performed on a
P
-node bidirectional ring in approximately P/2
steps.)
-
Extend the analysis and comparison of Exercise 13 to
account for competition for bandwidth in a 2-D mesh
architecture.
-
Develop a performance model for the systolic matrix multiplication
algorithm of Section 4.6, and use this to identify regimes
in which this algorithm is faster than the simpler algorithm based on
regular 2-D decompositions. Account for data reorganization costs.
-
Another matrix multiplication algorithm collects the matrices that
are to be multiplied on a single processor. Use performance models to
identify regimes in which this algorithm might be competitive.
Conduct empirical studies to validate your analytic results.
![[DBPP]](pictures//asm_color_tiny.gif)





![[Search]](pictures//search_motif.gif)
Next: Chapter Notes
Up: 4 Putting Components Together
Previous: 4.7 Summary
© Copyright 1995 by Ian Foster
 .
.
![[DBPP]](pictures//asm_color_tiny.gif)





![[Search]](pictures//search_motif.gif)
 .
.
![[DBPP]](pictures//asm_color_tiny.gif)





![[Search]](pictures//search_motif.gif)