Further Details: How to Measure Errors

The relative error $\vert \hat{\alpha} - \alpha \vert / \vert \alpha \vert$ in the approximation $\hat{\alpha}$ of the true solution $\alpha$ has a drawback: it often cannot be computed directly, because it depends on the unknown quantity $\vert \alpha \vert$ . However, we can often instead estimate $\vert \hat{\alpha} - \alpha \vert / \vert \hat{\alpha} \vert$ , since $\hat{\alpha}$ is known (it is the output of our algorithm). Fortunately, these two quantities are necessarily close together, provided either one is small, which is the only time they provide a useful bound anyway. For example, $\vert \hat{\alpha} - \alpha \vert / \vert \hat{\alpha} \vert \leq .1$ implies

$\begin{displaymath} .9 \frac{\vert \hat{\alpha} - \alpha \vert}{\vert \hat{\alph... ...\hat{\alpha} - \alpha \vert}{\vert \hat{\alpha} \vert} \; \; , \end{displaymath}$

Table 4.2 contains a variety of norms we will use to measure errors. These norms have the properties that $\Vert Ax\Vert _p \leq \Vert A\Vert _p \cdot \Vert x\Vert _p$ , and $\Vert AB\Vert _p \leq \Vert A\Vert _p \cdot \Vert B\Vert _p$ , where p is one of 1, 2, $\infty$ , and F. These properties are useful for deriving error bounds.

An error bound that uses a given norm may be changed into an error bound that uses another norm. This is accomplished by multiplying the first error bound by an appropriate function of the problem dimension. Table 4.3 gives the factors f_pq(n) such that $\Vert x \Vert _p \leq f_{pq}(n) \Vert x \Vert _q$ , where n is the dimension of x.

Values of f_pq(n) such that $\Vert x \Vert _p \leq f_{pq}(n) \Vert x \Vert _q$ , where x is an n-vector

**Table 4.3:** Bounding One Vector Norm in Terms of Another
		q
		1	2	$\infty$
	1	1	$\sqrt{n}$	n
p	2	1	1	$\sqrt{n}$
	$\infty$	1	1	1

Table 4.4 gives the factors f_pq(m,n) such that $\Vert A \Vert _p \leq f_{pq}(m,n) \Vert A \Vert _q$ , where A is m-by-n.

Values of f_pq(m,n) such that $\Vert A \Vert _p \leq f_{pq}(m,n) \Vert A \Vert _q$ , where A is m-by-n

**Table 4.4:** Bounding One Matrix Norm in Terms of Another
		q
		1	2	F	$\infty$
	1	1	$\sqrt{m}$	$\sqrt{m}$	m
p	2	$\sqrt{n}$	1	1	$\sqrt{m}$
	F	$\sqrt{n}$	$\sqrt{\min (m,n)}$	1	$\sqrt{m}$
	$\infty$	n	$\sqrt{n}$	$\sqrt{n}$	1

The two-norm of A, |A|₂, is also called the spectral norm of A, and is equal to the largest singular value $\sigma_{\max}(A)$ of A. We shall also need to refer to the smallest singular value $\sigma_{\min}(A)$ of A; its value can be defined in a similar way to the definition of the two-norm in Table 4.2, namely as $\min_{x \neq 0} \Vert Ax\Vert _2 / \Vert x\Vert _2$ when A has at least as many rows as columns, and defined as $\min_{x \neq 0} \Vert A^Tx\Vert _2 / \Vert x\Vert _2$ when A has more columns than rows. The two-norm, Frobenius norm , and singular values of a matrix do not change if the matrix is multiplied by a real orthogonal (or complex unitary) matrix.

Now we define subspaces spanned by more than one vector, and angles between subspaces. Given a set of k n-dimensional vectors $\{ x_1 , ... , x_k \}$ , they determine a subspace $\cal S$ consisting of all their possible linear combinations $\{ \sum_{i=1}^k \beta_i x_i$ , $\beta_i$ scalars }. We also say that $\{ x_1 , ... , x_k \}$ spans $\cal S$ . The difficulty in measuring the difference between subspaces is that the sets of vectors spanning them are not unique. For example, $\{ x \}$ , $\{ -x \}$ and $\{ 2x \}$ all determine the same subspace. This means we cannot simply compare the subspaces spanned by $\{ \hat{x}_1 , ... , \hat{x}_k \}$ and $\{ x_1 , ... , x_k \}$ by comparing each $\hat{x}_i$ to x_i. Instead, we will measure the angle between the subspaces, which is independent of the spanning set of vectors. Suppose subspace $\hat{\cal S}$ is spanned by $\{ \hat{x}_1 , ... , \hat{x}_k \}$ and that subspace $\cal S$ is spanned by $\{ x_1 , ... , x_k \}$ . If k=1, we instead write more simply $\{ \hat x \}$ and $\{ x \}$ . When k=1, we defined the angle $\theta (\hat{\cal S}, {\cal S})$ between $\hat{\cal S}$ and $\cal S$ as the acute angle between $\hat{x}$ and x. When k>1, we define the acute angle between $\hat{\cal S}$ and $\cal S$ as the largest acute angle between any vector $\hat{x}$ in $\hat{\cal S}$ , and the closest vector x in $\cal S$ to $\hat{x}$ :

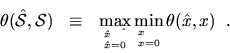
$\begin{eqnarray*} \theta (\hat{\cal S}, {\cal S}) & \equiv & \max_{\hat{x} \in {... ...min_{x \in {\cal S} \atop x \neq 0} \theta ( \hat{x},x ) \; \; . \end{eqnarray*}$

$\begin{displaymath} \theta ( \hat{\cal S}, {\cal S} ) = \arccos \sigma_{\min} ( \hat{X}^H X ) \; \; . \end{displaymath}$

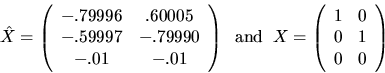
$\begin{displaymath} \hat{X} = \left( \begin{array}{cc} -.79996 & .60005 \\ -.599... ...\begin{array}{cc} 1 & 0 \\ 0 & 1 \\ 0 & 0 \end{array} \right) \end{displaymath}$

As stated above, all our bounds will contain a factor p(n) (or p(m,n)), which measure how roundoff errors can grow as a function of matrix dimension n (or m and m). In practice, the true error usually grows just linearly with n, but we can generally only prove much weaker bounds of the form p(n)=O(n³). This is because we can not rule out the extremely unlikely possibility of rounding errors all adding together instead of canceling on average. Using p(n) = O(n³) would give very pessimistic and unrealistic bounds, especially for large n, so we content ourselves with describing p(n) as a ``modestly growing'' polynomial function of n. Using p(n)=10n in the error bound formulas will often give a reasonable bound. For detailed derivations of various p(n), see [55,67,103].

There is also one situation where p(n) can grow as large as 2^n-1: Gaussian elimination. This typically occurs only on specially constructed matrices presented in numerical analysis courses [103, p. 212][67]. However, the expert drivers for solving linear systems, xGESVX and xGBSVX, provide error bounds incorporating p(n), and so this rare possibility can be detected.