



Next: How to Measure Errors
Up: Sources of Error in
Previous: Sources of Error
in Contents
Index
Further Details: Floating Point Arithmetic
Roundoff error is bounded in
terms of the machine precision 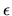 , which is the smallest value satisfying
, which is the smallest value satisfying
where a and b are floating-point numbers, 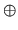 is any one of the four operations +, -, x and
is any one of the four operations +, -, x and 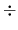 , and
, and 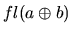 is the floating-point result of
is the floating-point result of 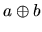 . Machine epsilon,
. Machine epsilon, 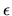 , is the smallest value for which this inequality is true for all
, is the smallest value for which this inequality is true for all 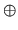 , and for all a and b such that
, and for all a and b such that 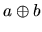 is neither too large (magnitude exceeds the overflow threshold) nor too small (is nonzero with magnitude
less than the underflow threshold) to
be represented accurately in the machine. We also assume
is neither too large (magnitude exceeds the overflow threshold) nor too small (is nonzero with magnitude
less than the underflow threshold) to
be represented accurately in the machine. We also assume 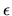 bounds the relative error in unary
operations like square root:
bounds the relative error in unary
operations like square root:
A precise characterization of 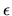 depends on the details of the machine arithmetic and sometimes even of the
compiler. For example, if addition and subtraction are implemented without
a guard digit4.1we
must redefine
depends on the details of the machine arithmetic and sometimes even of the
compiler. For example, if addition and subtraction are implemented without
a guard digit4.1we
must redefine 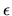 to be the smallest number such that
to be the smallest number such that
In order to assure portability, machine parameters
such as machine epsilon, the overflow threshold and underflow threshold are
computed at runtime by the auxiliary routine xLAMCH4.2. The alternative, keeping
a fixed table of machine parameter values, would degrade portability because
the table would have to be changed when moving from one machine, or even
one compiler, to another.
Actually, most machines, but not yet all, do have the same machine parameters
because they implement IEEE Standard Floating Point Arithmetic [4,5], which exactly specifies floating-point
number representations and operations. For these machines, including all
modern workstations and PCs4.3, the values of these parameters
are given in Table 4.1.
Table 4.1: Values of Machine Parameters in IEEE
Floating Point Arithmetic
| Machine parameter |
Single Precision (32 bits) |
Double Precision (64 bits) |
Machine epsilon 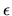 = xLAMCH('E')
= xLAMCH('E') |
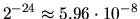
|
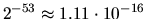
|
| Underflow threshold = xLAMCH('U') |
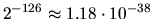
|
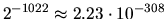
|
| Overflow threshold = xLAMCH('O') |
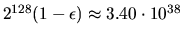
|
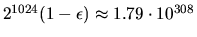
|
As stated above, we will ignore overflow and underflow in discussing
error bounds. References [24,67] discuss extending error bounds to include
underflow, and show that for many common computations, when underflow occurs
it is less significant than roundoff. With some important exceptions described
below, overflow usually means that a computation has failed so the error
bounds do not apply.
Therefore, most of our error bounds will simply be proportional to machine
epsilon. This means, for example, that if the same problem in solved in double
precision and single precision, the error bound in double precision will
be smaller than the error bound in single precision by a factor of
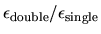 . In IEEE arithmetic, this ratio is
. In IEEE arithmetic, this ratio is
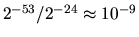 , meaning that one expects the double precision answer to have approximately
nine more decimal digits correct than the single precision answer.
, meaning that one expects the double precision answer to have approximately
nine more decimal digits correct than the single precision answer.
LAPACK routines are generally insensitive to the details of rounding
and exception handling, like their counterparts in LINPACK and EISPACK. One
algorithm, xLASV2, can return significantly
more accurate results if addition and subtraction have a guard digit, but
is still quite accurate if they do not (see the end of section 4.9).
However, several LAPACK routines do make assumptions about details of
the floating point arithmetic. We list these routines here.
- Infinity and NaN arithmetic. In IEEE arithmetic, there are specific
rules for evaluating quantities like 1/0 and 0/0. Overflowed
quantities and division-by-zero (like 1/0) result in a
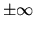 symbol, which continues to propagate through the computation using rules
like
symbol, which continues to propagate through the computation using rules
like 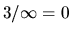 . In particular, there is no error message or termination of execution. Similarly,
quantities like 0/0 and
. In particular, there is no error message or termination of execution. Similarly,
quantities like 0/0 and 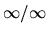 must be replaced by NaN (the ``Not a Number'' symbol) and propagated as
well. See [4,5] for details. The following LAPACK routines,
and the routines that call them, assume the presence of this infinity and
NaN arithmetic for their correct functioning:
must be replaced by NaN (the ``Not a Number'' symbol) and propagated as
well. See [4,5] for details. The following LAPACK routines,
and the routines that call them, assume the presence of this infinity and
NaN arithmetic for their correct functioning:
- xSTEGR, which computes eigenvalues and eigenvectors of symmetric
tridiagonal matrices. It is called by the drivers for the symmetric
and Hermitian eigenproblems xSYEVR, xHEEVR and xSTEVR.4.4
- Accuracy of add/subtract. If there is a guard digit in addition
and subtraction, or if there is no guard digit but addition and subtraction
are performed in the way they are on the Cray C90, Cray YMP, Cray XMP
or Cray 2, then we can guarantee that the following routines work correctly.
(They could theoretically fail on a hexadecimal or decimal machine without
a guard digit, but we know of no such machine.)
- xSTEDC, which uses divide-and-conquer to find the eigenvalues and
eigenvectors of a symmetric tridiagonal matrix. It is called by
all the drivers for the symmetric, Hermitian, generalized symmetric
definite and generalized Hermitian definite eigenvalue drivers with
names ending in -EVD or -GVD.
- xBDSDC, which uses divide-and-conquer to find the SVD
of a bidiagonal matrix. It is called by xGESDD.
- xLALSD, which uses divide-and-conquer to solve a bidiagonal least
squares problem with the SVD. It is called by xGELSD.




Next: How to Measure Errors
Up: Sources of Error in
Previous: Sources of Error
in Contents
Index
Susan Blackford
1999-10-01
![]() , which is the smallest value satisfying
, which is the smallest value satisfying
![]() depends on the details of the machine arithmetic and sometimes even of the
compiler. For example, if addition and subtraction are implemented without
a guard digit4.1we
must redefine
depends on the details of the machine arithmetic and sometimes even of the
compiler. For example, if addition and subtraction are implemented without
a guard digit4.1we
must redefine ![]() to be the smallest number such that
to be the smallest number such that ![]() . In IEEE arithmetic, this ratio is
. In IEEE arithmetic, this ratio is
![]() , meaning that one expects the double precision answer to have approximately
nine more decimal digits correct than the single precision answer.
, meaning that one expects the double precision answer to have approximately
nine more decimal digits correct than the single precision answer.