LAPACK Benchmark

This section contains performance numbers for selected LAPACK driver routines. These routines provide complete solutions for the most common problems of numerical linear algebra, and are the routines users are most likely to call:

• Solve an n-by-n system of linear equations with 1 right hand side using DGESV. side
• Find only the eigenvalues of an n-by-n nonsymmetric matrix using DGEEV.
• Find the eigenvalues and right eigenvectors of an n-by-n nonsymmetric matrix using
  DGEEV. DSYEVD. matrix using DSYEVD.
• Find only the singular values of an n-by-n matrix using DGESDD.
• Find the singular values and right and left singular vectors of an n-by-n matrix using
  DGESVD.
• Find the singular values and right and left singular vectors of an n-by-n matrix using
  DGESDD.

We only present data on DGESDD for singular values only, and not DGESVD, because both use the same algorithm. We include both DGESVD and DGESDD for computing all the singular values and singular vectors to illustrate the speedup of the new algorithm DGESDD over its predecessor DGESVD: For 1000-by-1000 matrices DGESDD is between 6 and 7 times faster than DGESVD on most machines.

The above drivers are timed on a variety of computers. In addition, we present data on fewer machines to compare the performance of the five different routines for solving linear least squares problems, and several different routines for the symmetric eigenvalue problem. Again, the purpose is to illustrate the performance improvements in LAPACK 3.0.

Data is provided for PCs, shared memory parallel computers, and high performance workstations. All timings were obtained by using the machine-specific optimized BLAS available on each machine. For machines running the Linux operating system, the ATLAS[102] BLAS were used. In all cases the data consisted of 64-bit floating point numbers (double precision). For each machine and each driver, a small problem (N=100 with LDA=101) and a large problem (N=1000 with LDA=1001) were run. Block sizes NB = 1, 16, 32 and 64 were tried, with data only for the fastest run reported in the tables below. For DGEEV, ILO=1 and IHI=N. The test matrices were generated with randomly distributed entries. All run times are reported in seconds, and block size is denoted by nb. The value of nb was chosen to make N=1000 optimal. It is not necessarily the best choice for N=100. See Section 6.2 for details.

The performance data is reported using three or four statistics. First, the run-time in seconds is given. The second statistic measures how well our performance compares to the speed of the BLAS, specifically DGEMM. This ``equivalent matrix multiplies'' statistic is calculated as

$\frac{\rm run-time(LAPACK~Driver~on~an~{\it n}-by-{\it n}~matrix)}{\rm run-time(DGEMM~used~to~multiply~two~{\it n}-by-{\it n}~matrices)}$

and labeled as $\frac{\rm Time}{\rm T(MM)}$ in the tables. The performance information for the BLAS routines
DGEMV (TRANS='N') and DGEMM (TRANSA='N', TRANSB='N') is provided in Table 3.12, along with the clock speed for each machine in Tables 3.2, 3.3, 3.4, 3.5, and 3.6. The third statistic is the true megaflop rating. For the eigenvalue and singular value drivers, a fourth ``synthetic megaflop'' statistic is also presented. We provide this statistic because the number of floating point operations needed to find eigenvalues and singular values depends on the input data, unlike linear equation solving or linear least squares solving with DGELS, and on the algorithm. The synthetic megaflop rating is defined to be a ``standard'' number of flops required to solve the problem, divided by the run-time in microseconds. This ``standard'' number of flops is taken to be the average for a standard algorithm over a variety of problems, as given in Table 3.13. In all cases we ignore terms of O(N²). The flop count in this table for the nonsymmetric eigenvalue problem assumes the unblocked algorithm is used, and that two QR sweeps are needed to deflate each eigenvalue [55]. The flop count for the symmetric eigenproblem and SVD assumes that all the work done on the tridiagonal and bidiagonal matrices is O(N²), as is the case with xSTEGR and will be the case with the SVD in the future.

We also include several figures comparing the speed of several routines for the symmetric eigenvalue problem and several least squares drivers to highlight the performance improvements in LAPACK 3.0.

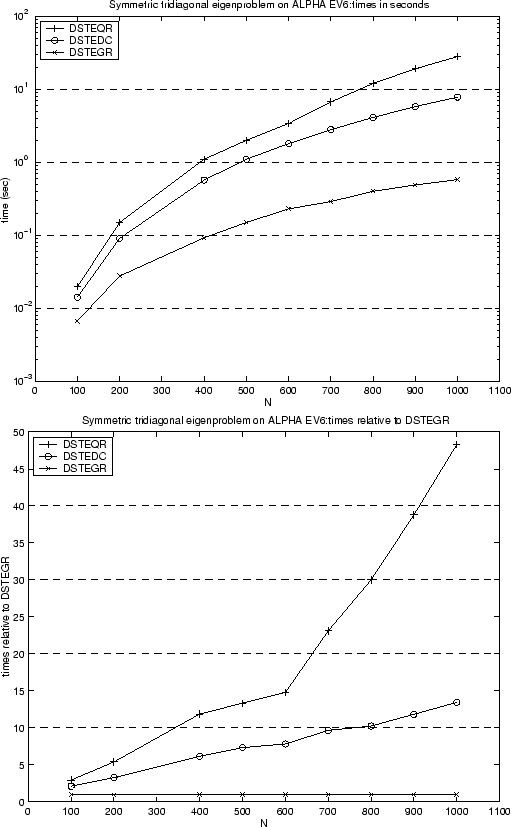
First consider Figure 3.1, which compares the performance of three routines, DSTEQR, DSTEDC and DSTEGR, for computing all the eigenvalues and eigenvectors of a symmetric tridiagonal matrix. The times are shown on a Compaq AlphaServer DS-20 for matrix dimensions from 100 to 1000. The symmetric tridiagonal matrix was obtained by taking a random dense symmetric matrix and reducing it to tridiagonal form (the performance can vary depending on the distribution of the eigenvalues of the matrix, but the data shown here is typical). DSTEQR (used in driver DSYEV) was the only algorithm available in LAPACK 1.0, DSTEDC (used in driver DSYEVD) was introduced in LAPACK 2.0, and DSTEGR (used in driver DSYEVR) was introduced in LAPACK 3.0. As can be seen, for large matrices DSTEGR is about 14 times faster than DSTEDC and nearly 50 times faster than DSTEQR.

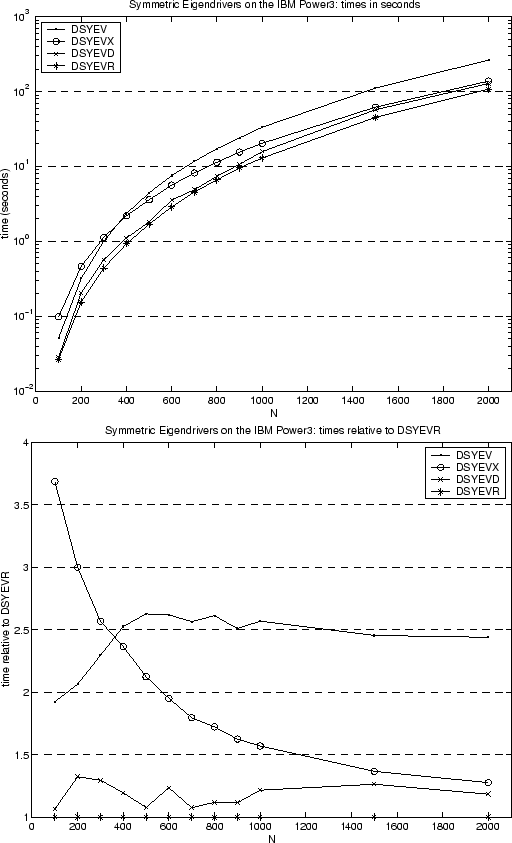
Next consider Figure 3.2, which compares the performance of four driver routines, DSYEV, DSYEVX, DSYEVD and DSYEVR, for computing all the eigenvalues and eigenvectors of a dense symmetric matrix. The times are shown on an IBM Power 3 for matrix dimensions from 100 to 2000. The symmetric matrix was chosen randomly. The cost of these drivers is essentially the cost of phases 1 and 3 (reduction to tridiagonal form and backtransformation) plus the cost of phase 2 (the symmetric tridiagonal eigenproblem) discussed in the last paragraph. Since the cost of phases 1 and 3 is large, performance differences in phase 2 are no longer as visible. We note that if we had chosen a test matrix with a large cluster of nearby eigenvalues, then the cost of DSYEVX would have been much larger, without significantly affecting the timings of the other drivers. DSYEVR is the driver of choice.

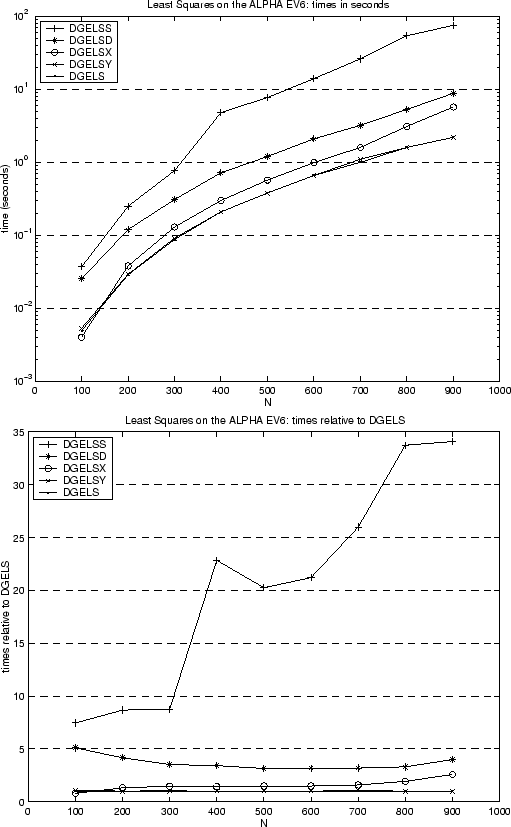
Finally consider Figure 3.3, which compares the performance of five drivers for the linear least squares problem, DGELS, DGELSY, DGELSX, DGELSD and DGELSS, which are shown in order of decreasing speed. DGELS is the fastest. DGELSY and DGELSX use QR with pivoting, and so handle rank-deficient problems more reliably than DGELS but can be more expensive. DGELSD and DGELSS use the SVD, and so are the most reliable (and expensive) ways to solve rank deficient least squares problems. DGELS, DGELSX and DGELSS were in LAPACK 1.0, and DGELSY and DGELSD were introduced in LAPACK 3.0. The times are shown on a Compaq AlphaServer DS-20 for squares matrices with dimensions from 100 to 1000, and for one right-hand-side. The matrices were chosen at random (which means they are full rank). First consider DGELSY, which is meant to replace DGELSX. We can see that the speed of DGELSY is nearly indistinguishable from the fastest routine DGELS, whereas DGELSX is over 2.5 times slower for large matrices. Next consider DGELSD, which is meant to replace DGELSS. It is 3 to 5 times slower than the fastest routine, DGELS, whereas its predecessor DGELSS was 7 to 34 times slower. Thus both DGELSD and DGELSY are significantly faster than their predecessors.

Figure 3.1: Timings of routines for computing all eigenvalues and eigenvectors of a symmetric tridiagonal matrix. The upper graph shows times in seconds on a Compaq AlphaServer DS-20. The lower graph shows times relative to the fastest routine DSTEGR, which appears as a horizontal line at 1.

Figure 3.2: Timings of driver routines for computing all eigenvalues and eigenvectors of a dense symmetric matrix. The upper graph shows times in seconds on an IBM Power3. The lower graph shows times relative to the fastest routine DSYEVR, which appears as a horizontal line at 1.

Figure 3.3: Timings of driver routines for the least squares problem. The upper graph shows times in seconds on a Compaq AlphaServer DS-20. The lower graph shows times relative to the fastest routine DGELS, which appears as a horizontal line at 1.

Table 3.12: Execution time and Megaflop rates for DGEMV and DGEMM

	DGEMV				DGEMM
	Values of n=m=k
	100		1000		100		1000
	Time	Mflops	Time	Mflops	Time	Mflops	Time	Mflops
Dec Alpha Miata	.0151	66	27.778	36	.0018	543	1.712	584
Compaq AlphaServer DS-20	.0027	376	8.929	112	.0019	522	2.000	500
IBM Power 3	.0032	304	2.857	350	.0018	567	1.385	722
IBM PowerPC	.0435	23	40.000	25	.0063	160	4.717	212
Intel Pentium II	.0075	134	16.969	59	.0031	320	3.003	333
Intel Pentium III	.0071	141	14.925	67	.0030	333	2.500	400
SGI O2K (1 proc)	.0046	216	4.762	210	.0018	563	1.801	555
SGI O2K (4 proc)	5.000	0.2	2.375	421	.0250	40	0.517	1936
Sun Ultra 2 (1 proc)	.0081	124	17.544	57	.0033	302	3.484	287
Sun Enterprise 450 (1 proc)	.0037	267	11.628	86	.0021	474	1.898	527

megaflop SSYEV/DSYEV.

Table 3.13: ``Standard'' floating point operation counts for LAPACK drivers for n-by-n matrices

Driver	Options	Operation
		Count
xGESV	1 right hand side	$.67 \cdot N^3$
xGEEV	eigenvalues only	$10.00 \cdot N^3$
xGEEV	eigenvalues and right eigenvectors	$26.33 \cdot N^3$
xGES{VD,DD}	singular values only	$2.67 \cdot N^3$
xGES{VD,DD}	singular values and left and right singular vectors	$6.67 \cdot N^3$

Table 3.14: Performance of DGESV for n-by-n matrices

	No. of		Values of n
	proc.	nb	100			1000
			Time	$\frac{\rm Time}{\rm T(MM)}$	Mflops	Time	$\frac{\rm Time}{\rm T(MM)}$	Mflops
Dec Alpha Miata	1	28	.004	2.2	164	1.903	1.11	351
Compaq AlphaServer DS-20	1	28	.002	1.05	349	1.510	0.76	443
IBM Power 3	1	32	.003	1.67	245	1.210	0.87	552
Intel Pentium II	1	40	.006	1.94	123	2.730	0.91	245
Intel Pentium III	1	40	.005	1.67	136	2.270	0.91	294
SGI Origin 2000	1	64	.003	1.67	227	1.454	0.81	460
SGI Origin 2000	4	64	.004	0.16	178	1.204	2.33	555
Sun Ultra 2	1	64	.008	2.42	81	5.460	1.57	122
Sun Enterprise 450	1	64	.006	2.86	114	3.698	1.95	181

Table 3.15: Performance of DGEEV, eigenvalues only

	No. of		Values of n
	proc.	nb	100				1000
					True	Synth			True	Synth
			Time	$\frac{\rm Time}{\rm T(MM)}$	Mflops	Mflops	Time	$\frac{\rm Time}{\rm T(MM)}$	Mflops	Mflops
Dec Alpha Miata	1	28	.157	87.22	70	64	116.480	68.04	81	86
Compaq AS DS-20	1	28	.044	23.16	423	228	52.932	26.47	177	189
IBM Power 3	1	32	.060	33.33	183	167	91.210	65.86	103	110
Intel Pentium II	1	40	.100	32.26	110	100	107.940	35.94	87	93
Intel Pentium III	1	40	.080	26.67	137	133	91.230	36.49	103	110
SGI Origin 2000	1	64	.074	41.11	148	135	54.852	30.46	172	182
SGI Origin 2000	4	64	.093	3.72	117	107	42.627	82.45	222	235
Sun Ultra 2	1	64	.258	78.18	43	38	246.151	70.65	38	41
Sun Enterprise 450	1	64	.178	84.76	62	56	163.141	85.95	57	61

Table 3.16: Performance of DGEEV, eigenvalues and right eigenvectors

	No. of		Values of n
	proc.	nb	100				1000
					True	Synth			True	Synth
			Time	$\frac{\rm Time}{\rm T(MM)}$	Mflops	Mflops	Time	$\frac{\rm Time}{\rm T(MM)}$	Mflops	Mflops
Dec Alpha Miata	1	28	.308	171.11	86	86	325.650	190.22	73	81
Compaq AS DS-20	1	28	.092	48.42	290	287	159.409	79.70	149	165
IBM Power 3	1	32	.130	72.22	204	203	230.650	166.53	103	114
Intel Pentium II	1	40	.200	64.52	133	132	284.020	94.58	84	93
Intel Pentium III	1	40	.170	56.67	156	155	239.070	95.63	100	110
SGI Origin 2000	1	64	.117	65.00	228	226	197.455	109.64	121	133
SGI Origin 2000	4	64	.159	6.36	167	166	146.975	284.28	164	179
Sun Ultra 2	1	64	.460	139.39	58	58	601.732	172.71	39	44
Sun Enterprise 450	1	64	.311	148.10	85	85	418.011	220.24	57	63

Table 3.17: Performance of DGESDD, singular values only

	No. of		Values of n
	proc.	nb	100				1000
					True	Synth			True	Synth
			Time	$\frac{\rm Time}{\rm T(MM)}$	Mflops	Mflops	Time	$\frac{\rm Time}{\rm T(MM)}$	Mflops	Mflops
Dec Alpha Miata	1	28	.043	23.89	61	61	36.581	21.37	73	73
Compaq AS DS-20	1	28	.011	5.79	236	236	11.789	5.89	226	226
IBM Power 3	1	32	.020	11.11	133	133	8.090	5.84	330	330
Intel Pentium II	1	40	.040	12.90	67	67	29.120	9.70	92	92
Intel Pentium III	1	40	.030	10.00	89	89	25.830	10.33	103	103
SGI Origin 2000	1	64	.024	13.33	113	113	12.407	6.89	215	215
SGI Origin 2000	4	64	.058	2.32	46	46	4.926	9.53	541	541
Sun Ultra 2	1	64	.088	26.67	30	30	60.478	17.36	44	44
Sun Enterprise 450	1	64	.060	28.57	92	45	47.813	25.19	56	56

Table 3.18: Performance of DGESVD, singular values and left and right singular vectors

	No. of		Values of n
	proc.	nb	100				1000
					True	Synth			True	Synth
			Time	$\frac{\rm Time}{\rm T(MM)}$	Mflops	Mflops	Time	$\frac{\rm Time}{\rm T(MM)}$	Mflops	Mflops
Dec Alpha Miata	1	28	.222	123.33	77	30	320.985	187.49	48	21
Compaq AS DS-20	1	28	.053	27.89	326	126	142.843	71.42	107	47
IBM Power 3	1	32	.070	38.89	245	95	251.940	181.91	61	26
Intel Pentium II	1	40	.150	48.39	114	44	282.550	94.09	54	24
Intel Pentium III	1	40	.120	40.00	142	56	244.690	97.88	62	27
SGI Origin 2000	1	64	.074	41.11	232	90	176.134	97.80	87	38
SGI Origin 2000	4	64	.145	5.80	118	46	198.656	384.25	77	34
Sun Ultra 2	1	64	.277	83.94	62	24	570.290	163.69	27	12
Sun Enterprise 450	1	64	.181	86.19	95	37	402.456	212.04	38	17

Table 3.19: Performance of DGESDD, singular values and left and right singular vectors

	No. of		Values of n
	proc.	nb	100				1000
					True	Synth			True	Synth
			Time	$\frac{\rm Time}{\rm T(MM)}$	Mflops	Mflops	Time	$\frac{\rm Time}{\rm T(MM)}$	Mflops	Mflops
Dec Alpha Miata	1	28	.055	30.56	123	121	47.206	27.57	141	141
Compaq AS DS-20	1	28	.021	11.05	310	318	20.658	10.33	323	323
IBM Power 3	1	32	.025	13.89	268	267	15.230	11.00	438	438
Intel Pentium II	1	40	.060	19.35	112	111	44.270	14.74	151	151
Intel Pentium III	1	40	.050	16.67	134	133	38.930	15.57	171	171
SGI Origin 2000	1	64	.035	19.44	189	191	24.985	13.87	267	267
SGI Origin 2000	4	64	.091	3.64	73	73	8.779	16.89	759	760
Sun Ultra 2	1	64	.149	45.15	45	45	93.417	26.81	72	71
Sun Enterprise 450	1	64	.102	48.57	66	65	70.597	37.20	94	94