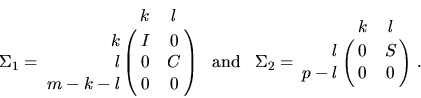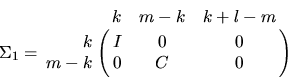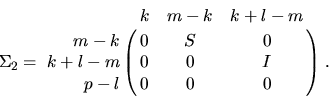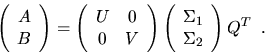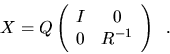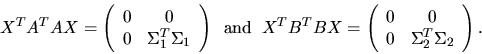



Next: Computational Routines
Up: Generalized Eigenvalue
and Singular Previous: Generalized Nonsymmetric Eigenproblems (GNEP)
Contents
Index
Generalized Singular Value Decomposition (GSVD)
The generalized (or quotient) singular
value decomposition of an m-by-n matrix A and a p-by-n
matrix B is given by the pair of factorizations
The matrices in these factorizations have the following properties:
- U is m-by-m, V is p-by-p, Q
is n-by-n, and all three matrices are orthogonal. If A
and B are complex, these matrices are unitary instead of orthogonal,
and QT should be replaced by QH
in the pair of factorizations.
- R is r-by-r, upper triangular and nonsingular.
[0,R] is r-by-n (in other words, the 0 is an r-by-n-r
zero matrix). The integer r is the rank of
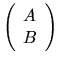 , and satisfies
, and satisfies 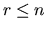 .
.
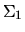 is m-by-r,
is m-by-r, 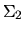 is p-by-r, both are real, nonnegative and diagonal, and
is p-by-r, both are real, nonnegative and diagonal, and
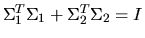 . Write
. Write
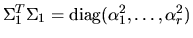 and
and
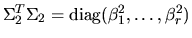 , where
, where 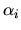 and
and 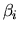 lie in the interval from 0 to 1. The ratios
lie in the interval from 0 to 1. The ratios
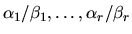 are called the generalized singular values of the pair A,
B. If
are called the generalized singular values of the pair A,
B. If 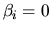 , then the generalized singular value
, then the generalized singular value
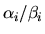 is infinite.
is infinite.
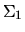 and
and 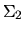 have the following detailed structures, depending on whether
have the following detailed structures, depending on whether 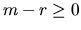 or m-r < 0. In the first case,
or m-r < 0. In the first case, 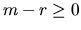 , then
, then
Here l is the rank of B, k=r-l, C
and S are diagonal matrices satisfying
C2 + S2 = I, and S is
nonsingular. We may also identify
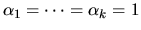 ,
, 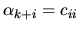 for
for 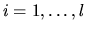 ,
, 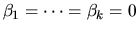 , and
, and 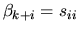 for
for 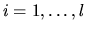 . Thus, the first k generalized singular values
. Thus, the first k generalized singular values
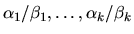 are infinite, and the remaining l generalized singular values are
finite.
are infinite, and the remaining l generalized singular values are
finite.
In the second case, when m-r < 0,
and
Again, l is the rank of B, k=r-l, C
and S are diagonal matrices satisfying C2 + S2
= I, S is nonsingular, and we may identify
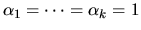 ,
, 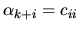 for
for 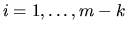 ,
, 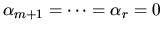 ,
, 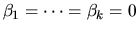 ,
, 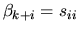 for
for 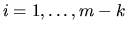 , and
, and 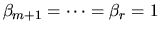 . Thus, the first k generalized singular values
. Thus, the first k generalized singular values
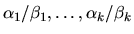 are infinite, and the remaining l generalized singular values are
finite.
are infinite, and the remaining l generalized singular values are
finite.
Here are some important special cases of the generalized singular value
decomposition. First, if B
is square and nonsingular, then r=n and the generalized singular
value decomposition of A and B is equivalent to the singular
value decomposition of AB-1, where the singular values
of AB-1 are equal to the generalized singular values of
the pair A, B:
Second, if the columns of 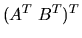 are orthonormal, then r=n, R=I and the generalized
singular value decomposition of A and B is equivalent to the
CS (Cosine-Sine) decomposition of
are orthonormal, then r=n, R=I and the generalized
singular value decomposition of A and B is equivalent to the
CS (Cosine-Sine) decomposition of 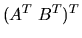 [55]:
[55]:
Third, the generalized eigenvalues and eigenvectors of
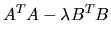 can be expressed in terms of the generalized singular value decomposition:
Let
can be expressed in terms of the generalized singular value decomposition:
Let
Then
Therefore, the columns of X are the eigenvectors of
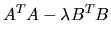 , and the ``nontrivial'' eigenvalues are the squares of the generalized singular
values (see also section 2.3.5.1).
``Trivial'' eigenvalues are those corresponding to the leading n-r
columns of X, which span the common null space of AT
A and BT B. The ``trivial eigenvalues'' are not well defined2.1.
, and the ``nontrivial'' eigenvalues are the squares of the generalized singular
values (see also section 2.3.5.1).
``Trivial'' eigenvalues are those corresponding to the leading n-r
columns of X, which span the common null space of AT
A and BT B. The ``trivial eigenvalues'' are not well defined2.1.
A single driver routine xGGSVD computes the generalized singular value
decomposition of A and B
(see Table 2.6). The method is
based on the method described in [83,10,8].
Table 2.6: Driver routines for generalized eigenvalue
and singular value problems
| Type of |
Function and storage scheme |
Single precision |
Double precision |
| problem |
|
real |
complex |
real |
complex |
| GSEP |
simple driver |
SSYGV |
CHEGV |
DSYGV |
ZHEGV |
| |
divide and conquer driver |
SSYGVD |
CHEGVD |
DSYGVD |
ZHEGVD |
| |
expert driver |
SSYGVX |
CHEGVX |
DSYGVX |
ZHEGVX |
| |
simple driver (packed storage) |
SSPGV |
CHPGV |
DSPGV |
ZHPGV |
| |
divide and conquer driver |
SSPGVD |
CHPGVD |
DSPGVD |
ZHPGVD |
| |
expert driver |
SSPGVX |
CHPGVX |
DSPGVX |
ZHPGVX |
| |
simple driver (band matrices) |
SSBGV |
CHBGV |
DSBGV |
ZHBGV |
| |
divide and conquer driver |
SSBGVD |
CHBGVD |
DSBGV |
ZHBGVD |
| |
expert driver |
SSBGVX |
CHBGVX |
DSBGVX |
ZHBGVX |
| GNEP |
simple driver for Schur factorization |
SGGES |
CGGES |
DGGES |
ZGGES |
| |
expert driver for Schur factorization |
SGGESX |
CGGESX |
DGGESX |
ZGGESX |
| |
simple driver for eigenvalues/vectors |
SGGEV |
CGGEV |
DGGEV |
ZGGEV |
| |
expert driver for eigenvalues/vectors |
SGGEVX |
CGGEVX |
DGGEVX |
ZGGEVX |
| GSVD |
singular values/vectors |
SGGSVD |
CGGSVD |
DGGSVD |
ZGGSVD |




Next: Computational Routines
Up: Generalized Eigenvalue
and Singular Previous: Generalized Nonsymmetric Eigenproblems (GNEP)
Contents
Index
Susan Blackford
1999-10-01
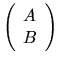 , and satisfies
, and satisfies ![]() and
and ![]() have the following detailed structures, depending on whether
have the following detailed structures, depending on whether ![]() or m-r < 0. In the first case,
or m-r < 0. In the first case, ![]() , then
, then