



Next: Installing LAPACK
Routines Up: Documentation
and Software Conventions Previous: Real Diagonal Elements of Contents Index
Representation of Orthogonal or Unitary Matrices
A real orthogonal or complex unitary matrix (usually denoted Q)
is often represented in LAPACK as a product of elementary
reflectors -- also referred to as elementary Householder matrices (usually denoted
Hi). For example,
Most users need not be aware of the details, because LAPACK routines are
provided to work with this representation:
- routines whose names begin SORG- (real) or CUNG- (complex) can generate
all or part of Q explicitly;
- routines whose name begin SORM- (real) or CUNM- (complex) can multiply
a given matrix by Q or QH without
forming Q explicitly.
The following further details may occasionally be useful.
An elementary reflector (or elementary Householder matrix) H
of order n is a unitary matrix of the form
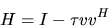
|
(5.1) |
where 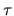 is a scalar, and v is an n-vector, with
is a scalar, and v is an n-vector, with
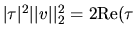 ); v is often referred to as the Householder vector . Often v has several leading or trailing
zero elements, but for the purpose of this discussion assume that H
has no such special structure.
); v is often referred to as the Householder vector . Often v has several leading or trailing
zero elements, but for the purpose of this discussion assume that H
has no such special structure.
There is some redundancy in the representation (5.1), which can be removed in various ways.
The representation used in LAPACK (which differs from those used in LINPACK
or EISPACK) sets v1 = 1; hence v1
need not be stored. In real arithmetic,
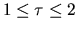 , except that
, except that 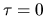 implies H = I.
implies H = I.
In complex arithmetic, 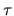 may be complex, and satisfies
may be complex, and satisfies
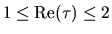 and
and 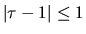 . Thus a complex H is not Hermitian (as it is in other representations),
but it is unitary, which is the important property. The advantage of allowing
. Thus a complex H is not Hermitian (as it is in other representations),
but it is unitary, which is the important property. The advantage of allowing
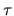 to be complex is that, given an arbitrary complex vector x,
H can be computed so that
to be complex is that, given an arbitrary complex vector x,
H can be computed so that
with real 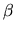 . This is useful, for example, when reducing a complex Hermitian matrix to
real symmetric tridiagonal form, or a complex rectangular
matrix to real bidiagonal form.
. This is useful, for example, when reducing a complex Hermitian matrix to
real symmetric tridiagonal form, or a complex rectangular
matrix to real bidiagonal form.
For further details, see Lehoucq [79].




Next: Installing LAPACK
Routines Up: Documentation
and Software Conventions Previous: Real Diagonal Elements of Contents Index
Susan Blackford
1999-10-01
![]() , except that
, except that ![]() implies H = I.
implies H = I. ![]() may be complex, and satisfies
may be complex, and satisfies
![]() and
and ![]() . Thus a complex H is not Hermitian (as it is in other representations),
but it is unitary, which is the important property. The advantage of allowing
. Thus a complex H is not Hermitian (as it is in other representations),
but it is unitary, which is the important property. The advantage of allowing
![]() to be complex is that, given an arbitrary complex vector x,
H can be computed so that
to be complex is that, given an arbitrary complex vector x,
H can be computed so that