We start by stating the simplest error bounds for individual eigenvalues and eigenvectors and leave the more complicated ones to subsequent subsections.
As discussed in section 2.4.8 ,
from a computational point of view it is more natural to define
the generalized nonsymmetric eigenvalue problem in
the form
![]() with
with
![]() instead of
instead of
![]() .
The eigenvalue
.
The eigenvalue ![]() is represented
as a pair
is represented
as a pair
![]() ,
where a finite
eigenvalue has
,
where a finite
eigenvalue has ![]() and an infinite eigenvalue has
and an infinite eigenvalue has ![]() .
As in the standard nonsymmetric eigenvalue problem we have both right
and left eigenvectors
.
As in the standard nonsymmetric eigenvalue problem we have both right
and left eigenvectors ![]() and
and ![]() ,
respectively, defined as
,
respectively, defined as
Now we state our error bounds.
Let
![]() be the eigenvalues of (A, B),
let xi be a right eigenvector corresponding to
be the eigenvalues of (A, B),
let xi be a right eigenvector corresponding to
![]() :
:
![]() and let
and let
![]() and
and ![]() be the corresponding eigenvalues and
eigenvectors computed by the expert driver routine
xGGEVX (see subsection 2.3.5.2).
be the corresponding eigenvalues and
eigenvectors computed by the expert driver routine
xGGEVX (see subsection 2.3.5.2).
The approximate error bounds4.10for the computed eigenvalues are
These bounds can be computed by the following code fragment:
EPSMCH = SLAMCH( 'E' )
* Compute the generalized eigenvalues and eigenvectors of (A,B)
* ALPHAR/BETA contains the real parts of the eigenvalues
* ALPHAI/BETA contains the imaginary parts of the eigenvalues
* VL contains the left eigenvectors
* VR contains the right eigenvectors
CALL SGGEVX( 'P', 'V', 'V', 'B', N, A, LDA, B, LDB, ALPHAR,
$ ALPHAI, BETA, VL, LDVL, VR, LDVR, ILO, IHI, LSCALE,
$ RSCALE, ABNRM, BBNRM, RCONDE, RCONDV, WORK, LWORK,
$ IWORK, BWORK, INFO )
IF( INFO.GT.0 ) THEN
PRINT *,'INFO =', info, ' from SGGEVX.'
ELSE IF( N.GT.0 ) THEN
ABNORM = SLAPY2( ABNRM, BBNRM )
DO 10 I = 1,N
EERRBD(I) = EPSMCH*ABNORM/RCONDE(I)
VERRBD(I) = EPSMCH*ABNORM/RCONDV(I)
10 CONTINUE
END IF
For example, suppose4.1SLAMCH('E')
![]() and
and
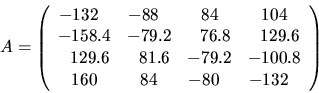
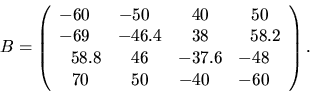
For this problem, the exact eigenvalues, eigenvectors, and eigenvalue condition numbers are known. Then the true eigenvalues, computed eigenvalues, approximate error bounds, and true error bounds are given in the following table.
| i | 1 | 2 | 3 | 4 |
| 1 | 2 | 3 | 4 | |
|
|
|
|
|
|
EERRBD(i) |
|
|
|
|
|
|
|
|
|
|
VERRBD(i) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|