Singular Eigenproblems

In this section, we give a brief discussion of singular matrix pairs (A,B).

If the determinant of $A - \lambda B$ is zero for all values of $\lambda$ (or the determinant of $\beta A - \alpha B$ is zero for all $(\alpha,\beta)$ ), the pair (A,B) is said to be singular. The eigenvalue problem of a singular pair is much more complicated than for a regular pair.

Consider for example the singular pair

$$A = \left( \begin{array}{cc} 1 & 0 \\ 0 & 0 \\ \end{array... ...t( \begin{array}{cc} 1 & 0 \\ 0 & 0 \\ \end{array} \right),$$

which has one finite eigenvalue 1 and one indeterminate eigenvalue 0/0. To see that neither eigenvalue is well determined by the data, consider the slightly different problem

$$A' = \left( \begin{array}{cc} 1 & \epsilon_1 \\ \epsilon_2 ... ...c} 1 & \epsilon_3 \\ \epsilon_4 & 0 \\ \end{array} \right),$$

where the $\epsilon_i$ are tiny nonzero numbers. Then it is easy to see that (A',B') is regular with eigenvalues $\epsilon_1 / \epsilon_3$ and $\epsilon_2 / \epsilon_4$ . Given any two complex numbers $\lambda_1$ and $\lambda_2$ , we can find arbitrarily tiny $\epsilon_i$ such that $\lambda_1 = \epsilon_1 / \epsilon_3$ and $\lambda_2 = \epsilon_2 / \epsilon_4$ are the eigenvalues of (A',B'). Since, in principle, roundoff could change (A,B) to (A',B'), we cannot hope to compute accurate or even meaningful eigenvalues of singular problems, without further information.

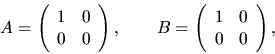
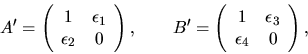
It is possible for a pair (A,B) in Schur form to be very close to singular, and so have very sensitive eigenvalues, even if no diagonal entries of A or B are small. It suffices, for example, for A and B to nearly have a common null space (though this condition is not necessary). For example, consider the 16-by-16 matrices

$$A'' = \left( \begin{array}{ccccc} 0.1 & 1 & & & \\ & 0.1 ... ...end{array} \right) \quad\quad \mbox{and} \quad\quad B'' = A''.$$

Changing the (n,1) entries of A'' and B'' to 10^-16, respectively, makes both A and B singular, with a common null vector. Then, using a technique analogous to the one applied to (A,B) above, we can show that there is a perturbation of A'' and B'' of norm $10^{-16} + \epsilon$ , for any $\epsilon>0$ , that makes the 16 perturbed eigenvalues have any arbitrary 16 complex values.

A complete understanding of the structure of a singular eigenproblem (A,B) requires a study of its Kronecker canonical form, a generalization of the Jordan canonical form. In addition to Jordan blocks for finite and infinite eigenvalues, the Kronecker form can contain ``singular blocks'', which occur only if ${\rm det}(A- \lambda B) \equiv 0$ for all $\lambda$ (or if A and B are nonsquare). See [53,93,105,97,29] for more details. Other numerical software, called GUPTRI, is available for computing a generalization of the Schur canonical form for singular eigenproblems [30,31].

The error bounds discussed in this guide hold for regular pairs only (they become unbounded, or otherwise provide no information, when (A,B) is close to singular). If a (nearly) singular pencil is reported by the software discussed in this guide, then a further study of the matrix pencil should be conducted, in order to determine whether meaningful results have been computed.