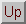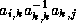 is nonzero, and fill is not allowed in position
is nonzero, and fill is not allowed in position 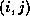 ,
instead of simply discarding this fill quantity subtract it from
the diagonal element
,
instead of simply discarding this fill quantity subtract it from
the diagonal element 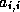 .
Such a factorization scheme is usually called a ``modified incomplete
factorization''.
.
Such a factorization scheme is usually called a ``modified incomplete
factorization''.

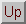



One modification to the basic idea of incomplete factorizations is as
follows:
If the product 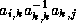 is nonzero, and fill is not allowed in position
is nonzero, and fill is not allowed in position 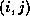 ,
instead of simply discarding this fill quantity subtract it from
the diagonal element
,
instead of simply discarding this fill quantity subtract it from
the diagonal element 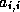 .
Such a factorization scheme is usually called a ``modified incomplete
factorization''.
.
Such a factorization scheme is usually called a ``modified incomplete
factorization''.
Mathematically this corresponds to forcing the preconditioner to have
the same rowsums as the original matrix.
One reason for considering modified incomplete factorizations is the
behavior of the spectral condition number of the preconditioned
system. It was mentioned above that for second order elliptic
equations the condition number of the
coefficient matrix is 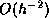 as a function of the discretization
mesh width. This order of magnitude is preserved by simple incomplete
factorizations, although usually a reduction by a large constant
factor is obtained.
as a function of the discretization
mesh width. This order of magnitude is preserved by simple incomplete
factorizations, although usually a reduction by a large constant
factor is obtained.
Modified factorizations are of interest because, in
combination with small perturbations, the spectral condition number of
the preconditioned system can be of a lower order.
It was first proved by Dupont, Kendall and
Rachford [81] that
a modified incomplete factorization of 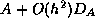 gives
gives
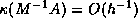 for the central difference case. More
general proofs are given by Gustafsson [112],
Axelsson and Barker [.2]AxBa:febook, and
Beauwens [32][31].
for the central difference case. More
general proofs are given by Gustafsson [112],
Axelsson and Barker [.2]AxBa:febook, and
Beauwens [32][31].
Instead of keeping row sums constant, one can also keep column
sums constant.
In computational fluid mechanics this idea is justified with the argument
that the material balance stays constant over all iterates.
(Equivalently, one wishes to avoid `artificial
diffusion'.)
Appleyard and Cheshire [4] observed that if 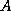 and
and 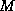 have the same column sums, the choice
have the same column sums, the choice

guarantees
that the sum of the elements in 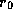 (the material balance error) is
zero, and that all further
(the material balance error) is
zero, and that all further 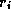 have elements summing to zero.
have elements summing to zero.
Modified incomplete factorizations can break down, especially when the variables are numbered other than in the natural row-by-row ordering. This was noted by Chan and Kuo [50], and a full analysis was given by Eijkhout [86] and Notay [161].
A slight variant of modified incomplete factorizations consists of the
class of ``relaxed incomplete factorizations''. Here the fill is
multiplied by a parameter 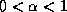 before it is subtracted from
the diagonal; see
Ashcraft and Grimes [11],
Axelsson and Lindskog [19][18],
Chan [44],
Eijkhout [86],
Notay [162],
Stone [194], and
Van der Vorst [204].
For the dangers of MILU in the presence of rounding error, see
Van der Vorst [206].
before it is subtracted from
the diagonal; see
Ashcraft and Grimes [11],
Axelsson and Lindskog [19][18],
Chan [44],
Eijkhout [86],
Notay [162],
Stone [194], and
Van der Vorst [204].
For the dangers of MILU in the presence of rounding error, see
Van der Vorst [206].