 like the Jacobi preconditioner, can be derived from the coefficient
matrix without any work.
like the Jacobi preconditioner, can be derived from the coefficient
matrix without any work.




The SSOR preconditioner like the Jacobi preconditioner, can be derived from the coefficient
matrix without any work.
like the Jacobi preconditioner, can be derived from the coefficient
matrix without any work.
If the original, symmetric, matrix is decomposed as

in its diagonal, lower, and upper triangular part, the SSOR matrix is defined as
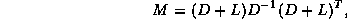
or, parameterized by 
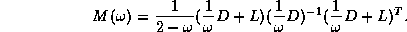
The optimal value of the  parameter, like the
parameter in the SOR method, will reduce the number
of iterations to a lower order.
Specifically, for second order elliptic problems a spectral
condition number
parameter, like the
parameter in the SOR method, will reduce the number
of iterations to a lower order.
Specifically, for second order elliptic problems a spectral
condition number 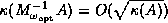 is attainable
(see Axelsson and Barker [.4]AxBa:febook). In practice,
however, the spectral
information needed to calculate the optimal
is attainable
(see Axelsson and Barker [.4]AxBa:febook). In practice,
however, the spectral
information needed to calculate the optimal  is prohibitively
expensive to compute.
is prohibitively
expensive to compute.
The SSOR matrix is given in factored form, so this preconditioner shares many properties of other factorization-based methods (see below). For instance, its suitability for vector processors or parallel architectures depends strongly on the ordering of the variables. On the other hand, since this factorization is given a priori, there is no possibility of breakdown as in the construction phase of incomplete factorization methods.