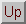and
and  must be selected so that they define a family of
ellipses
with common center
must be selected so that they define a family of
ellipses
with common center 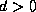 and foci
and foci 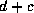 and
and  which contain the
ellipse that encloses the spectrum (or more general, field of values)
of
which contain the
ellipse that encloses the spectrum (or more general, field of values)
of 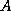 and for which the rate
and for which the rate  of
convergence is minimal:
of
convergence is minimal:

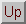



Comparing the pseudocode for Chebyshev Iteration with the pseudocode for the Conjugate Gradient method shows a high degree of similarity, except that no inner products are computed in Chebyshev Iteration .
Scalars  and
and  must be selected so that they define a family of
ellipses
with common center
must be selected so that they define a family of
ellipses
with common center 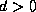 and foci
and foci 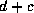 and
and  which contain the
ellipse that encloses the spectrum (or more general, field of values)
of
which contain the
ellipse that encloses the spectrum (or more general, field of values)
of 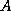 and for which the rate
and for which the rate  of
convergence is minimal:
of
convergence is minimal:
where  is the length of the
is the length of the  -axis of the ellipse.
-axis of the ellipse.
We provide code in which it is assumed that
the ellipse degenerate to the interval 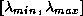 ,
that is all eigenvalues are real.
For code including the adaptive determination of the iteration
parameters
,
that is all eigenvalues are real.
For code including the adaptive determination of the iteration
parameters  and
and  the reader is referred
to Ashby [7].
the reader is referred
to Ashby [7].
The Chebyshev
method has the advantage over GMRES that only short recurrences are
used. On the other hand, GMRES is guaranteed to generate the smallest
residual over the current search space. The BiCG methods, which also
use short recurrences, do not minimize the residual in a suitable
norm; however, unlike Chebyshev iteration, they do not require
estimation of parameters (the spectrum of 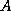 ). Finally, GMRES and
BiCG may be more effective in practice, because of superlinear
convergence behavior , which cannot be expected for
Chebyshev.
). Finally, GMRES and
BiCG may be more effective in practice, because of superlinear
convergence behavior , which cannot be expected for
Chebyshev.
For symmetric positive definite systems the ``ellipse'' enveloping the
spectrum degenerates to the interval 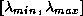 on the positive
on the positive  -axis, where
-axis, where 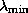 and
and
 are the smallest and largest eigenvalues of
are the smallest and largest eigenvalues of
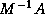 . In circumstances where the computation of inner products
is a bottleneck , it may be advantageous to start
with CG, compute
estimates of the extremal eigenvalues from the CG coefficients, and
then after sufficient convergence of these approximations switch to
Chebyshev Iteration . A similar strategy
may be adopted for a switch from GMRES, or BiCG-type methods, to
Chebyshev Iteration.
. In circumstances where the computation of inner products
is a bottleneck , it may be advantageous to start
with CG, compute
estimates of the extremal eigenvalues from the CG coefficients, and
then after sufficient convergence of these approximations switch to
Chebyshev Iteration . A similar strategy
may be adopted for a switch from GMRES, or BiCG-type methods, to
Chebyshev Iteration.