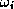 (see the algorithm). One such alternative is
Bi-CGSTAB2 (see Gutknecht [115]); more general
approaches are suggested by Sleijpen and Fokkema in [190].
(see the algorithm). One such alternative is
Bi-CGSTAB2 (see Gutknecht [115]); more general
approaches are suggested by Sleijpen and Fokkema in [190].




Bi-CGSTAB often converges about as fast as CGS,
sometimes faster and
sometimes not. CGS can be viewed as a method in which the BiCG
``contraction'' operator is applied twice. Bi-CGSTAB can be
interpreted as the product of BiCG and repeatedly applied GMRES(1). At
least locally, a residual vector is minimized , which leads to a
considerably smoother convergence behavior. On the
other hand, if the
local GMRES(1) step stagnates, then the Krylov subspace
is not
expanded, and Bi-CGSTAB will break down . This is a breakdown situation
that can occur in addition to the other breakdown possibilities in the
underlying BiCG algorithm. This type of breakdown may be avoided by
combining BiCG with other methods, i.e., by selecting other
values for 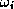 (see the algorithm). One such alternative is
Bi-CGSTAB2 (see Gutknecht [115]); more general
approaches are suggested by Sleijpen and Fokkema in [190].
(see the algorithm). One such alternative is
Bi-CGSTAB2 (see Gutknecht [115]); more general
approaches are suggested by Sleijpen and Fokkema in [190].
Note that Bi-CGSTAB has two stopping tests: if the method has already
converged at the first test on the norm of  , the subsequent update
would be numerically questionable. Additionally, stopping on the first
test saves a few unnecessary operations, but this is of minor importance.
, the subsequent update
would be numerically questionable. Additionally, stopping on the first
test saves a few unnecessary operations, but this is of minor importance.