 ) for positive definite
symmetric systems. The MINRES
and SYMMLQ
methods are variants that can
be applied to symmetric indefinite systems.
) for positive definite
symmetric systems. The MINRES
and SYMMLQ
methods are variants that can
be applied to symmetric indefinite systems.




The Conjugate Gradient method can be viewed as a special variant of
the Lanczos method
(see § ) for positive definite
symmetric systems. The MINRES
and SYMMLQ
methods are variants that can
be applied to symmetric indefinite systems.
) for positive definite
symmetric systems. The MINRES
and SYMMLQ
methods are variants that can
be applied to symmetric indefinite systems.
The vector sequences in the Conjugate Gradient method
correspond to a
factorization of a tridiagonal matrix similar to the coefficient
matrix. Therefore, a breakdown of the algorithm can occur
corresponding to a zero pivot if the matrix is indefinite.
Furthermore, for indefinite matrices the minimization property of the
Conjugate Gradient method is no longer well-defined. The
MINRES
and SYMMLQ
methods are variants of the CG method that avoid the
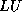 -factorization and do not suffer from breakdown. MINRES
minimizes
the residual in the
-factorization and do not suffer from breakdown. MINRES
minimizes
the residual in the 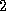 -norm . SYMMLQ solves the projected
system, but
does not minimize anything (it keeps the residual orthogonal to all
previous ones ). The convergence
behavior of Conjugate Gradients and MINRES for indefinite systems was
analyzed by Paige, Parlett, and Van der Vorst [167].
-norm . SYMMLQ solves the projected
system, but
does not minimize anything (it keeps the residual orthogonal to all
previous ones ). The convergence
behavior of Conjugate Gradients and MINRES for indefinite systems was
analyzed by Paige, Parlett, and Van der Vorst [167].
Breakdown: The occurrence of a zero coefficient that is to be used as a divisor in an iterative method.