

1.3. Использование библиотеки ScaLAPACK
Библиотека ScaLAPACK требует, чтобы все объекты (векторы и матрицы), являющиеся параметрами подпрограмм, были предварительно распределены по процессорам. Исходные объекты классифицируются как глобальные объекты, и параметры, описывающие их, хранятся в специальном описателе объекта - дескрипторе. Дескриптор некоторого распределенного по процессорам глобального объекта представляет собой массив целого типа, в котором хранится вся необходимая информация об исходном объекте. Части этого объекта, находящиеся в памяти какого-либо процессора, и их параметры являются локальными данными.
Для того, чтобы воспользоваться драйверной или вычислительной подпрограммой из библиотеки ScaLAPACK, необходимо выполнить 4 шага:
Библиотека подпрограмм ScaLAPACK поддерживает работу с матрицами трех типов:
Для каждого из этих типов используется различная топология сетки процессоров и различная схема распределения данных по процессорам. Эти различия обуславливают использование четырех типов дескрипторов. Дескриптор - массив целого типа, состоящий из 9 или 7 элементов в зависимости от типа дискриптора. Тип дескриптора, который используется для описания объекта, хранится в первой ячейке самого дескриптора. В таблице 1.1 приведены возможные значения типов дескрипторов.
| Тип дескриптора | Назначение |
| 1 | Заполненные матрицы |
| 501 | Ленточные и трехдиагональные матрицы |
| 502 | Матрица правых частей для уравнений с ленточными и трехдиагональными матрицами |
| 601 | Заполненные матрицы на внешних носителях |
Инициализация сетки процессоров
Для объектов, которые описываются дескриптором типа 1, распределение по процессорам производится на двумерную сетку процессоров. На рис. 1.2 представлен пример двумерной сетки размера 2 х 3 из 6 процессоров.
| 0 | 1 | 2 | |||||||
| 0 1 |
|
||||||||
Рис. 1.2. Пример двумерной сетки из 6 процессоров.
При таком распределении процессоры имеют двойную нумерацию:
Связь между сквозной и координатной нумерациями определяется параметром процедуры при инициализации сетки (нумерация вдоль строк - row-major или вдоль столбцов - column-major).
Инициализация сетки процессоров выполняется с помощью подпрограмм из библиотеки BLACS. Ниже приводится формат вызовов этих подпрограмм:
Для ленточных и трехдиагональных матриц (дескриптор 501) используется одномерная сетка процессоров (1 x NPROCS), т.е. параметр NPROW = 1, а NPCOL = NPROCS.
Для объектов, описываемых дескриптором 502 (правые части уравнений с ленточными и трехдиагональными матрицами), используется транспонированная одномерная сетка (NPROCS x 1). Работа с матрицами на внешних носителях (дескриптор 601) в данном пособии не рассматривается.
Распределение матрицы на сетку процессоров
Способ распределения матрицы на сетку процессоров также зависит от типа распределяемого объекта. Для заполненных матриц (тип дескриптора 1) принят блочно-циклический способ распределения данных по процессорам. При таком распределении матрица разбивается на блоки размера MB x NB, где MB - размер блока по строкам, а NB - по столбцам, и эти блоки циклически раскладываются по процессорам. Проиллюстрируем это на конкретном примере распределения матрицы общего вида A(9,9), т.е. M=9, N=9, на сетке процессоров NPROW x NPCOL = 2 х 3 при условии, что размер блока MB x NB = 2 х 2.
Разбиение исходной матрицы на блоки требуемого размера будет выглядеть следующим образом (рис. 1,3):
| a11 a12 a21 a22 |
a13 a14 a23 a24 |
a15 a16 a25 a26 |
a17 a18 a27 a28 |
a19 a29 |
| a31 a32 a41 a42 |
a33 a34 a43 a44 |
a35 a36 a45 a46 |
a37 a38 a47 a48 |
a39 a49 |
| a51 a52 a61 a62 |
a53 a54 a63 a64 |
a55 a56 a65 a66 |
a57 a58 a67 a68 |
a59 a69 |
| a71 a72 a81 a82 |
a73 a74 a83 a84 |
a75 a76 a85 a86 |
a77 a78 a87 a88 |
a79 a89 |
| a91 a92 | a93 a94 | a95 a96 | a97 a98 | a99 |
Рис. 1.3. Разбиение исходной матрицы на блоки размера 2x2.
После циклического распределения блоков вдоль строк и столбцов сетки процессоров получим следующее распределение матричных элементов по процессорам (рис. 1,4):
| 0 | 1 | 2 | |
| 0 | a11 a12 a17 a18 a21 a22 a27 a28 a51 a52 a57 a58 a61 a62 a67 a68 a91 a92 a97 a98 |
a13 a14 a19 a23 a24 a29 a53 a54 a59 a63 a64 a69 a93 a94 a99 |
a15 a16 a25 a26 a55 a56 a65 a66 a95 a96 |
| 1 | a31 a32 a37 a38 a41 a42 a47 a48 a71 a72 a77 a78 a81 a82 a87 a88 |
a33 a34 a39 a43 a44 a49 a73 a74 a79 a83 a84 a89 |
a35 a36 a45 a46 a75 a76 a85 a86 |
Рис. 1.4. Распределение элементов матрицы на сетке процессоров 2x3.
Следует иметь в виду, что описанная выше процедура - это не более чем наглядная иллюстрация сути вопроса. На самом деле полная матрица A и ее разбиение на блоки (рис. 1.4.) существует только в нашем воображении. В реальности задача состоит в том, чтобы в каждом процессоре сформировать массивы заведомо меньшей размерности, чем исходная матрица, и заполнить эти массивы матричными элементами в соответствии с принятыми параметрами распределения. Точное значение - сколько строк и столбцов должно находиться в каждом процессоре - позволяет вычислить подпрограмма-функция NUMROC из библиотеки PTOOLS, формат вызова которой приводится ниже:
NP = NUMROC (M, MB, MYROW, RSRC, NPROW)
NQ = NUMROC (N, NB, MYCOL, CSRC, NPCOL)
Здесь
NP - число строк в локальных подматрицах в строке процессоров MYROW;
NQ - число столбцов в локальных подматрицах в столбце процессоров MYCOL.
Входные параметры:
| M, | N | - | число строк и столбцов исходной матрицы; |
| MB, | NB | - | размеры блоков по строкам и по столбцам; |
| MYROW, | MYCOL | - | координаты процессора в сетке процессоров; |
| IRSRC, | ICSRC | - | координаты процессора, начиная с которого выполнено распределение матрицы (подразумевается возможность распределения не по всем процессорам); |
| NPROW, | NPCOL | - | число строк и столбцов в сетке процессоров. |
Важно также уметь оценить верхние значения величин NP и NQ для правильного описания размерностей локальных массивов. Можно использовать, например, такие формулы:
NROW = (M-1)/NPROW+MB
NCOL = (N-1)/NPCOL+NB
Дескриптор для данного типа матриц - это массив целого типа из 9 элементов. Он может быть заполнен либо непосредственно с помощью операторов присваивания, либо с помощью специальной подпрограммы из библиотеки PTOOLS. Описание назначения полей дескриптора и присваиваемых им значений приводится в следующей таблице.
| DESC(1) = | 1 | - | тип дескриптора; |
| DESC(2) = | ICTXT | - | контекст ансамбля процессоров; |
| DESC(3) = | M | - | число строк исходной матрицы; |
| DESC(4) = | N | - | число столбцов исходной матрицы; |
| DESC(5) = | MB | - | размер блока по строкам; |
| DESC(6) = | NB | - | размер блока по столбцам; |
| DESC(7) = | IRSRC | - | номер строки в сетке процессоров, начиная с которой распределяется матрица (обычно 0); |
| DESC(8) = | ICSRC | - | номер столбца в сетке процессоров, начиная с которого распределяется матрица (обычно 0); |
| DESC(9) = | NROW | - | число строк в локальной матрице (leading dimension). |
Вызов подпрограммы из PTOOLS, выполняющей аналогичное действие по формированию дескрипторов, имеет вид:
CALL DESCINIT(DESC, M, N, MB, NB, IRSRC, ICSRC, ICTXT, NROW, INFO)
Параметр INFO - статус возврата. Если INFO = 0, то подпрограмма выполнилась успешно; INFO = -I означает, что I-й параметр некорректен.
В расчетных формулах при решении задач линейной алгебры, как правило, фигурируют выражения, содержащие матричные элементы, идентифицируемые их глобальными индексами (I, J). После распределения матрицы по процессорам, а точнее, при заполнении локальных матриц на каждом процессоре, мы имеем дело с локальными индексами (i,j), поэтому очень важно знать связь между локальными и глобальными индексами. Так, если в сетке процессоров NPROW строк, а размер блока вдоль строк равен MB, то i-я строка локальных подматриц в MYROW строке сетки процессоров должна быть заполнена I-ми элементами строки исходной матрицы.
Формула для вычисления индекса I имеет вид:
I = MYROW*MB + ((i -1)/MB)*NPROW*MB + mod(i-1, MB) + 1,
Аналогично можно записать формулу для индесов столбцов:
J = MYCOL*NB + ((j -1)/NB)*NPCOL*NB + mod(j - 1,NB) + 1.
Здесь деление подразумевает деление нацело, а функция mod вычисляет остаток
от деления.
Симметричные и эрмитовы матрицы на сетке процессоров хранятся в виде полных матриц, однако используется при этом либо верхний, либо нижний треугольники. Поэтому в процедурах, работающих с такими матрицами, указывается параметр UPLO = 'U' для верхнего треугольника или UPLO = 'L' для нижнего треугольника.
Совершенно другой принцип распределения по процессорам принят для ленточных
и трехдиагональных матриц. В этом случае используется блочный принцип распределения. В каждом процессоре хранится только один блок, размер которого выбирается из соображений равномерности распределения, т.е. NB ![]() N/NPROCS. При этом объекты левой части уравнения распределяются по
столбцам, а правой - по строкам.
N/NPROCS. При этом объекты левой части уравнения распределяются по
столбцам, а правой - по строкам.
На рис. 1.5 представлен пример ленточной матрицы A(7,7).
| A = | 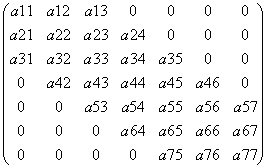 |
Рис. 1.5. Пример ленточной матрицы 7х7.
Для характеристики ленточных матриц вводится параметр ширины ленты BW для симметричных матриц и два параметра BWL (ширина поддиагонали) и BWU (ширина наддиагонали) для несимметричных матриц. Так для рассмотренного на рис. 1.5 примера:
Кроме того, если матрица несимметричная, то возможны два варианта факторизации этой матрицы: без выбора главного элемента и с выбором главного элемента столбца. В обоих случаях матрицы хранятся в виде прямоугольных матриц и распределяются по столбцам, однако в первом случае количество строк матрицы равно BWL+BWU + 1, а во втором 2*(BWL+BWU) +1.
Схема хранения матричных элементов несимметричной матрицы при использовании процедур "без выбора главных элементов" в 3-х процессорах при условии NB = 3 представлена на рис. 1.6. Звездочками отмечены неиспользуемые позиции.
| 0 | 1 | 2 | |||||||||||||||||||||||||||||||||||
|
|
|
Рис. 1.6. Распределение по процессорам несимметричной ленточной матрицы "без выбора главного элемента".
При использовании процедур с "выбором главного элемента" необходимо предусмотреть выделение дополнительной памяти для рабочих ячеек. Схема распределения матричных элементов в этом случае представлена на рис. 1.7, где через F обозначена дополнительная память.
| 0 | 1 | 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
Рис. 1.7. Распределение по процессорам несимметричной ленточной матрицы "с выбором главного элемента".
В случае, когда матрица A является симметричной положительно определенной, достаточно хранить либо нижние поддиагонали (рис. 1.8), либо верхние (рис. 1.9).
| 0 | 1 | 2 | |||||||||||||||||||||
|
|
|
Рис. 1.8. Распределение по процессорам симметричной положительно определенной ленточной матрицы (UPLO = 'L').
| 0 | 1 | 2 | |||||||||||||||||||||
|
|
|
Рис. 1.9. Распределение по процессорам симметричной положительно определенной ленточной матрицы (UPLO = 'U').
Трехдиагональные матрицы хранятся в виде трех векторов (DU,D,DL) в случае несимметричных матриц (рис. 1.10) и двух векторов (D,E) для симметричных матриц (рис. 1.11, 1.12).
| 0 | 1 | 2 | |||||||||||||||||||||||||
|
|
|
|
Рис. 1.10. Пример распределения по процессорам несимметричной трехдиагональной матрицы
Для симметричных матриц в вектор E могут заноситься либо поддиагональные элементы (рис. 1.11), либо наддиагональные (рис. 1.12).
| 0 | 1 | 2 | |||||||||||||||||
|
|
|
|
Рис. 1.11. Пример распределения по процессорам симметричной трехдиагональной матрицы (UPLO = 'L').
| 0 | 1 | 2 | |||||||||||||||||
|
|
|
|
Рис. 1.12. Пример распределения по процессорам симметричной трехдиагональной матрицы (UPLO = 'U').
Для всех рассмотренных выше матриц в качестве дескриптора используется массив целого типа из 7 элементов. Его заполнение выполняется напрямую с помощью операторов присваивания в соответствии со следующей таблицей:
| DESC(1)= | 501 | - | тип дескриптора; |
| DESC(2)= | ICTXT | - | контекст ансамбля процессоров; |
| DESC(3)= | N | - | число столбцов исходной матрицы; |
| DESC(4)= | NB | - | размер блока по столбцам; |
| DESC(5)= | ICSRC | - | номер столбца в сетке процессоров, начиная с которого распределяется матрица (обычно 0); |
| DESC(6)= | NROW | - | число строк в локальной матрице (leading dimension); |
| NROW = BWL+BWU+1 для несимметричных матриц в "без выбора главного элемента"; | |||
| NROW = 2*(BWL+BWU)+1 для несимметричных матриц в процедурах "с выбором главного элемента"; | |||
| NROW = BW+1 для симметричных положительно определенных матриц; | |||
| NROW - не используется для трехдиагональных матриц; | |||
| DESC(7) | - | не используется. |
Дескриптор для правых частей (табл. 1.4) имеет такую же структуру, как и для левых. Отличие состоит в том, что разложение по процессорам производится не по столбцам, а по строкам. Кроме того, во избежание лишних пересылок данных его параметры должны соответствовать параметрам дескриптора для левых частей:
| DESC(1)= | 502 | - | тип дескриптора; |
| DESC(2)= | ICTXT | - | контекст ансамбля процессоров; |
| DESC(3)= | M | - | число строк исходной матрицы (M = N); |
| DESC(4)= | MB | - | размер блока по строкам (MB = NB); |
| DESC(5)= | IRSRC | - | номер столбца в сетке процессоров, начиная с которого распределяется матрица (обычно 0); |
| DESC(6)= | NROW | - | число строк в локальной матрице (leading dimension) (NROW = NB); |
| DESC(7) | - | не используется. |
Обращения к подпрограммам библиотеки ScaLAPACK
Обращение к подпрограммам ScaLAPACK рассмотрим на примере вызова подпрограммы решения систем линейных алгебраических уравнений с матрицами общего вида. Имя подпрограммыа PDGESV указывает, что:
Обращение к подпрограмме имеет вид:
CALL PDGESV(N, NRHS, A, IA, JA, DESCA, IPIV, B, IB, JB, DESCB, INFO)
Здесь
| N | - | размерность исходной матрицы A (полной); |
| NRHS | - | количество правых частей в системе (сколько столбцов в матрице B); |
| А | - | на входе локальная часть распределенной матрицы A, на выходе локальная часть LU разложения; |
| IA, JA | - | индексы левого верхнего элемента подматрицы матрицы А, для которой находится решение (т.е. подразумевается возможность решать систему не для полной матрицы, а для ее части); |
| DESCA | - | дескриптор матрицы А (подробно рассмотрен выше); |
| IPIV | - | рабочий массив целого типа, который на выходе содержит информацию о перестановках в процессе факторизации. Длина массива должна быть не меньше количества строк в локальной подматрице; |
| B | - | на входе локальная часть распределенной матрицы B, на выходе локальная часть полученного решения (если решение найдено); |
| IB, JB | - | то же самое, что IA, JA для матрицы А; |
| DESCB | - | дескриптор матрицы B; |
| INFO | - | целая переменная, которая на выходе содержит информацию о том, успешно или нет завершилась подпрограмма, и причину аварийного завершения. |
Примерно такой же набор параметров используется для всех драйверных и вычислительных подпрограмм. Назначение их достаточно понятно, следует только внимательно следить за тем, какие параметры относятся к исходным (глобальным) объектам, а какие имеют локальный характер (в первую очередь это касается размерностей массивов и векторов). Подробную информацию обо всех подпрограммах ScaLAPACK можно найти на WWW серверах [2].
Освобождение сетки процессоров
Программы, использующие пакет ScaLAPACK, должны заканчиваться закрытием всех BLACS-процессов. Это осуществляется с помощью вызова подпрограмм:
CALL BLACS_GRIDEXIT (ICTXT) - закрытие контекста;
CALL BLACS_EXIT (0) - закрытие всех BLACS процессов.
Примечание: Кроме перечисленных подпрограмм в библиотеку BLACS входят подпрограммы пересылки данных, синхронизации процессов, выполнения глобальных операций по всему ансамблю процессоров или его части (строке или столбцу). Это позволяет обойтись без использования каких-либо других коммуникационных библиотек, тем не менее, допускается и совместное использование BLACS с другими коммуникационными библиотеками. Полное описание подпрограмм библиотеки BLACS включено в документацию по пакету ScaLAPACK [2].