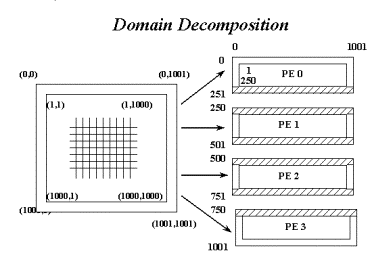
Еще одна область задач, для которых достаточно хорошо разработана технология параллельного программирования - это краевые задачи. В этом случае используется техника декомпозиции по процессорам расчетной области, как правило, с перекрытием подобластей. На рис. 8.3 представлено такое разложение исходной расчетной области на 4 процессора с топологией одномерной сетки. Заштрихованные области на каждом процессоре обозначают те точки, в которых расчет не производится, но они необходимы для выполнения расчета в пограничных точках. В них должна быть предварительно помещена информация с пограничного слоя соседнего процессора.

Рис. 8.3. Пример декомпозиции двумерной расчетной области

Приведем пример программы решения уравнения Лапласа методом Якоби на двумерной регулярной сетке. В программе декомпозиция области выполнена не по строкам, как на рисунке, а по столбцам. Так удобнее при программировании на языке FORTRAN, на C удобнее разбиение производить по строкам (это определяется способом размещения матриц в памяти компьютера).

С Программа решения уравнения Лапласа методом Якоби
С с использованием функции MPI_Sendrecv и NULL процессов
    PROGRAM JACOBI
    IMPLICIT NONE
    INCLUDE 'mpif.h'
    INTEGER n,m,npmin,nps,itmax
C Параметры:
С n      - количество точек области в каждом направлении;
С npmin  - минимальное число процессоров для решения задачи;
С npsаа  - число столбцов локальной части матрицы. Этот параметр
С          введен в целях экономии памяти;
С itmax  - максимальное число итераций, если сходимость не будет
С          достигнута.
    PARAMETER (n = 400, npmin=1, nps=n/npmin+1, itmax = 1000)
    REAL*8 A(0:n+1,0:nps+1), B(n,nps)
    REAL*8 diffnorm, gdiffnorm, eps, time
    INTEGER left, right, i, j, k, itcnt, status(0:3), tag
    INTEGER IAM, NPROCS, ierr
    LOGICAL converged
С Определение числа процессоров, выделенных задаче (NPROCS),
C и номера текущего процессора (IAM)
    CALL MPI_INIT(IERR)
    CALL MPI_COMM_SIZE(MPI_COMM_WORLD, NPROCS, ierr)
    CALL MPI_COMM_RANK(MPI_COMM_WORLD, IAM, ierr)
С Установка критерия достижения сходимости
    eps = 0.01
С Вычисление числа столбцов, обрабатываемых процессором
    m = n/NPROCS
    IF (IAM.LT.(n-NPROCS*m)) THEN
    m = m+1
    END IF
    time = MPI_Wtime()
С Задание начальных и граничных значений
    do j = 0,m+1
    do i = 0,n+1
     a(i,j) = 0.0
    end do
    end do

    do j = 0,m+1
    A(0,j) = 1.0
    A(n+1,j) = 1.0
    end do
    IF(IAM.EQ.0) then
    do i = 0,n+1
    A(i,0) = 1.0
    end do
    end if
    IF(IAM.EQ.NPROCS-1) then
    do i = 0,n+1
    A(i,m+1) = 1.0
    end do
    end if
С Определение номеров процессоров слева и справа. Если таковые
С отсутствуют, то им присваивается значение MPI_PROC_NULL
С (для них коммуникационные операцииа игнорируются)
    IF (IAM.EQ.0) THEN
    left = MPI_PROC_NULL
    ELSE
    left = IAM - 1
    END +IF
    IF (IAM.EQ.NPROCS-1) THEN
    right = MPI_PROC_NULL
    ELSE
    right = IAM+1
    END IF
    tag = 100
    itcnt = 0
    converged = .FALSE.
С Цикл по итерациям
    DO k = 1,itmax
    diffnorm = 0.0
    itcnt = itcnt + 1
С Вычисление новых значений функции по 5-точечной схеме
    DO j = 1, m
    DO i = 1, n
    B(i,j)=0.25*(A(i-1,j)+A(i+1,j)+A(i,j-1)+A(i,j+1))
    diffnorm = diffnorm + (B(i,j)-A(i,j))**2
    END DO
    END DO
С Переприсваивание внутренних точек области
    DO j = 1, m
    DO i = 1, n
    A(i,j) = B(i,j)
    END DO
    END DO

С Пересылка граничных значений в соседние процессоры
    CALL MPI_SENDRECV(B(1,1), n, MPI_DOUBLE_PRECISION, left, tag,
    $ A(1,0), n, MPI_DOUBLE_PRECISION, left, tag, MPI_COMM_WORLD,
    $ status, ierr)

    CALL MPI_SENDRECV(B(1,m), n, MPI_DOUBLE_PRECISION, right,
    $ tag, A(1,m+1), n, MPI_DOUBLE_PRECISION, right, tag,
    $ MPI_COMM_WORLD, status, ierr)
С Вычисление невязки и проверка условия достижения сходимости
    CALL MPI_Allreduce( diffnorm, gdiffnorm, 1, MPI_DOUBLE_PRECISION,
    $ MPI_SUM, MPI_COMM_WORLD, ierr )
    gdiffnorm = sqrt( gdiffnorm)
    converged = gdiffnorm.LT.eps
    if(converged) goto 777
    END DO
 777 continue

    time = MPI_Wtime() - time
    IF(IAM.EQ.0) then
    WRITE(*,*) ' At iteration ', itcnt, 'а diff is ', gdiffnorm
    WRITE(*,*) ' Time calculation: ', time
    END IF   
    CALL MPI_Finalize(ierr)
    stop
    end