Error Bounds for the Generalized Symmetric Definite Eigenproblem

There are three types of problems to consider. In all cases A and B are real symmetric (or complex Hermitian) and B is positive definite. These decompositions are computed for real symmetric matrices by the driver routines xSYGV, xSYGVX, xSYGVD, xSPGV, xSPGVX, xSPGVD, and (for type 1 only) xSBGV, xSBGVX and xSBGVD (see subsection 2.3.5.1). These decompositions are computed for complex Hermitian matrices by the driver routines xHEGV, xHEGVX, xHEGVD, xHPGV, xHPGVX, xHPGVD, and (for type 1 only) xHBGV, xHBGVX, xHBGVD (see subsection 2.3.5.1). In each of the following three decompositions, $\Lambda$ is real and diagonal with diagonal entries $\lambda_1 \leq \cdots \leq \lambda_n$, and the columns z_i of Z are linearly independent vectors. The $\lambda_i$ are called eigenvalues and the z_i are eigenvectors.

1.

$A - \lambda B$. The eigendecomposition may be written $Z^T A Z = \Lambda$ and Z^T B Z = I (or $Z^H A Z = \Lambda$ and Z^H B Z = I if A and B are complex). This may also be written $Az_i = \lambda_i B z_i$.

2.

$AB- \lambda I$. The eigendecomposition may be written $Z^{-1} A Z^{-T} = \Lambda$ and Z^T B Z = I ( $Z^{-1} A Z^{-H} = \Lambda$ and Z^H B Z = I if A and B are complex). This may also be written $ABz_i = \lambda_i z_i$.

3.

$BA- \lambda I$. The eigendecomposition may be written $Z^T A Z = \Lambda$ and Z^T B^-1 Z = I ( $Z^H A Z = \Lambda$ and Z^H B^-1 Z = I if A and B are complex). This may also be written $BAz_i = \lambda_i z_i$.

The approximate error bounds^4.10for the computed eigenvalues $\hat{\lambda}_1 \leq \cdots \leq \hat{\lambda}_n$ are

$$\vert \hat{\lambda}_i - \lambda_i \vert \leq {\tt EERRBD}(i) \; .$$

The approximate error bounds for the computed eigenvectors $\hat{z}_i$, which bound the acute angles between the computed eigenvectors and true eigenvectors z_i, are

$$\theta ( \hat{z}_i , z_i ) \leq {\tt ZERRBD} (i) \; .$$

These bounds are computed differently, depending on which of the above three problems are to be solved. The following code fragments show how.

1.

First we consider error bounds for problem 1.

      EPSMCH = SLAMCH( 'E' )
*     Solve the eigenproblem A - lambda B (ITYPE = 1)
      ITYPE = 1
*     Compute the norms of A and B
      ANORM = SLANSY( '1', UPLO, N, A, LDA, WORK )
      BNORM = SLANSY( '1', UPLO, N, B, LDB, WORK )
*     The eigenvalues are returned in W
*     The eigenvectors are returned in A
      CALL SSYGV( ITYPE, 'V', UPLO, N, A, LDA, B, LDB, W, WORK,
     $            LWORK, INFO )
      IF( INFO.GT.0 .AND. INFO.LE.N ) THEN
         PRINT *,'SSYGV did not converge'
      ELSE IF( INFO.GT.N ) THEN
         PRINT *,'B not positive definite'
      ELSE IF ( N.GT.0 ) THEN
*        Get reciprocal condition number RCONDB of Cholesky factor of B
         CALL STRCON( '1', UPLO, 'N', N, B, LDB, RCONDB, WORK, IWORK,
     $                INFO )
         RCONDB = MAX( RCONDB, EPSMCH )
         CALL SDISNA( 'Eigenvectors', N, N, W, RCONDZ, INFO )
         DO 10 I = 1, N
            EERRBD( I ) = ( EPSMCH / RCONDB**2 ) * ( ANORM / BNORM +
     $                      ABS( W(I) ) )
            ZERRBD( I ) = ( EPSMCH / RCONDB**3 ) * ( ( ANORM / BNORM )
     $                     / RCONDZ(I) + ( ABS( W(I) ) / RCONDZ(I) ) *
     $                     RCONDB )
10       CONTINUE
      END IF

For example^4.11, if ${\tt SLAMCH('E')} = 2^{-24} = 5.961 \cdot 10^{-8}$,

$$A = \left( \begin{array}{ccc} 100000 & 10099 & 2109 \\ 10099... ...& 10 & 2 \\ 10 & 100 & 10 \\ 2 & 10 & 100 \end{array} \right)$$

then ${\tt ANORM} = 120231$, ${\tt BNORM} = 120$, and ${\tt RCONDB} = .8326$, and the approximate eigenvalues, approximate error bounds, and true errors are

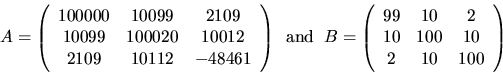
i	$\lambda_i$	EERRBD(i)	true $\vert \hat{\lambda}_i - \lambda_i \vert$	ZERRBD(i)	true $\theta ( \hat{v}_i , v_i )$
1	-500.0	$1.3 \cdot 10^{-4}$	$9.0 \cdot 10^{-6}$	$9.8 \cdot 10^{-8}$	$1.0 \cdot 10^{-9}$
2	1000.	$1.7 \cdot 10^{-4}$	$4.6 \cdot 10^{-5}$	$1.9 \cdot 10^{-5}$	$1.2\cdot10^{-7}$
3	1010.	$1.7 \cdot 10^{-4}$	$1.0 \cdot 10^{-4}$	$1.9 \cdot 10^{-5}$	$1.1 \cdot 10^{-7}$

This code fragment cannot be adapted to use xSBGV (or xHBGV), because xSBGV does not return a conventional Cholesky factor in B, but rather a ``split'' Cholesky factorization (performed by xPBSTF).

2.

Problem types 2 and 3 have the same error bounds. We illustrate only type 2.

      EPSMCH = SLAMCH( 'E' )
*     Solve the eigenproblem A*B - lambda I (ITYPE = 2)
      ITYPE = 2
*     Compute the norms of A and B
      ANORM = SLANSY( '1', UPLO, N, A, LDA, WORK )
      BNORM = SLANSY( '1', UPLO, N, B, LDB, WORK )
*     The eigenvalues are returned in W
*     The eigenvectors are returned in A
      CALL SSYGV( ITYPE, 'V', UPLO, N, A, LDA, B, LDB, W, WORK,
     $            LWORK, INFO )
      IF( INFO.GT.0 .AND. INFO.LE.N ) THEN
         PRINT *,'SSYGV did not converge'
      ELSE IF( INFO.GT.N ) THEN
         PRINT *,'B not positive definite'
      ELSE IF ( N.GT.0 ) THEN
*        Get reciprocal condition number RCONDB of Cholesky factor of B
         CALL STRCON( '1', UPLO, 'N', N, B, LDB, RCONDB, WORK, IWORK,
     $                INFO )
         RCONDB = MAX( RCONDB, EPSMCH )
         CALL SDISNA( 'Eigenvectors', N, N, W, RCONDZ, INFO )
         DO 10 I = 1, N
            EERRBD(I) = ( ANORM * BNORM ) * EPSMCH +
     $                  ( EPSMCH / RCONDB**2 ) * ABS( W(I) )
            ZERRBD(I) = ( EPSMCH / RCONDB ) * ( ( ANORM * BNORM ) /
     $                    RCONDZ(I) + 1.0 / RCONDB )
10       CONTINUE
      END IF

For the same A and B as above, the approximate eigenvalues, approximate error bounds, and true errors are

i	$\lambda_i$	EERRBD(i)	true $\vert \hat{\lambda}_i - \lambda_i \vert$	ZERRBD(i)	true $\theta ( \hat{v}_i , v_i )$
1	$-4.817 \cdot 10^6$	1.3	$6.0 \cdot 10^{-3}$	$1.7 \cdot 10^{-7}$	$7.0 \cdot 10^{-9}$
2	$8.094 \cdot 10^6$	1.6	1.5	$3.4 \cdot 10^{-7}$	$3.3 \cdot 10^{-8}$
3	$1.219 \cdot 10^7$	1.9	4.5	$3.4 \cdot 10^{-7}$	$4.7 \cdot 10^{-8}$