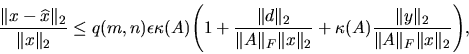



Next: Error Bounds for
the Up: General Linear
Model Problem Previous: General Linear Model Problem Contents Index
Further Details: Error Bounds for General Linear Model Problems
In this subsection, we will summarize the available error bounds. The
reader may also refer to [2,13,50,80] for further details.
Let 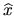 and
and 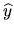 be the solutions by the driver routine xGGGLM (see subsection 4.6). Then
be the solutions by the driver routine xGGGLM (see subsection 4.6). Then 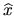 is normwise backward stable and
is normwise backward stable and 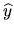 is stable in a mixed forward/backward sense [13]. Specifically, we have
is stable in a mixed forward/backward sense [13]. Specifically, we have 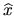 and
and 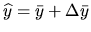 , where
, where 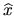 and
and 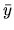 solve
solve
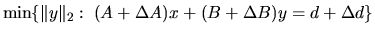 , and
, and
and q(m,n,p) is a modestly growing function
of m, n, and p. We take q(m,n,p)
= 1 in the code fragment above. Let 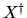 denote the Moore-Penrose pseudo-inverse of X. Let
denote the Moore-Penrose pseudo-inverse of X. Let
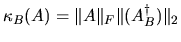 ( = CNDAB above) and
( = CNDAB above) and
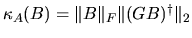 ( = CNDBA above) where
( = CNDBA above) where 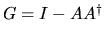 and
and ![$A^\dagger_B = A^\dagger[I-B(GB)^\dagger]$](img512.gif) . When
. When 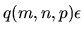 is small, the errors
is small, the errors 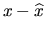 and
and 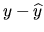 are bounded by
are bounded by
When B = I, the GLM problem is the standard LS problem.
y is the residual vector y = d - Ax,
and we have
and
where
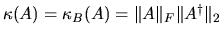 and
and 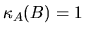 . The error bound of
. The error bound of 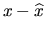 is the same as in the LSE problem (see section 4.6.1.1), which is essentially
the same as given in section 4.5.1. The bound on the error in
is the same as in the LSE problem (see section 4.6.1.1), which is essentially
the same as given in section 4.5.1. The bound on the error in 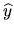 is the same as that provided in [55, section
5.3.7].
is the same as that provided in [55, section
5.3.7].




Next: Error Bounds for
the Up: General Linear
Model Problem Previous: General Linear Model Problem Contents Index
Susan Blackford
1999-10-01
![]() and
and ![]() be the solutions by the driver routine xGGGLM (see subsection 4.6). Then
be the solutions by the driver routine xGGGLM (see subsection 4.6). Then ![]() is normwise backward stable and
is normwise backward stable and ![]() is stable in a mixed forward/backward sense [13]. Specifically, we have
is stable in a mixed forward/backward sense [13]. Specifically, we have ![]() and
and ![]() , where
, where ![]() and
and ![]() solve
solve
![]() , and
, and 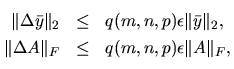
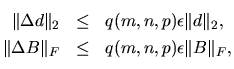
![\begin{eqnarray*}
\frac{ \Vert x-\widehat {x} \Vert _2 }{ \Vert x \Vert _2 } & ...
...ght)
+ \Vert B \Vert _F \Vert (GB)^\dagger \Vert _2 ^2 \bigg] .
\end{eqnarray*}](img515.gif)