Further Details: Error Bounds for Linear Equation Solving

The conventional error analysis of linear equation solving goes as follows. Let Ax=b be the system to be solved. Let $\hat{x}$ be the solution computed by LAPACK (or LINPACK) using any of their linear equation solvers. Let r be the residual $r = b - A \hat{x}$ . In the absence of rounding error r would be zero and $\hat{x}$ would equal x; with rounding error one can only say the following:

The normwise backward error of the computed solution $\hat{x}$ , with respect to the infinity norm, is the pair E,f which minimizes

$$\max \left( \frac{\Vert E \Vert _{\infty}}{\Vert A \Vert _{\... ...frac{\Vert f \Vert _{\infty}}{\Vert b \Vert _{\infty}} \right)$$

subject to the constraint $(A+E)\hat{x}=b+f$ . The minimal value of $\max \left( \frac{\Vert E \Vert _{\infty}}{\Vert A \Vert _{\infty}} , \frac{\Vert f \Vert _{\infty}}{\Vert b \Vert _{\infty}} \right)$ is given by

$$\omega_{\infty}= \frac{\Vert r \Vert _{\infty}}{\Vert A \Ver... ...t \Vert \hat{x} \Vert _{\infty}+ \Vert b \Vert _{\infty}} \; .$$

One can show that the computed solution $\hat{x}$ satisfies $\omega_{\infty}\leq p(n) \cdot \epsilon$ , where p(n) is a modestly growing function of n. The corresponding condition number is $\kappa_{\infty}(A) \equiv \Vert A\Vert _{\infty}\cdot \Vert A^{-1}\Vert _{\infty}$ . The error $x-\hat{x}$ is bounded by

$$\frac{\Vert x- \hat{x} \Vert _{\infty}}{\Vert x \Vert _{\inf... ...dot \omega_{\infty}\cdot \kappa_{\infty}(A) = {\tt ERRBD} \; .$$

In the first code fragment in the last section, $2 \cdot \omega_{\infty}$ , which is $4.504 \cdot 10^{-8}$ in the numerical example, is approximated by $\epsilon = 2^{-24} = 5.960 \cdot 10^{-8}$ . Approximations of $\kappa_{\infty}(A)$ -- or, strictly speaking, its reciprocal RCOND -- are returned by computational routines xyyCON (subsection 2.4.1) or driver routines xyySVX (subsection 2.3.1). The code fragment makes sure RCOND is at least $\epsilon =$ EPSMCH to avoid overflow in computing ERRBD. This limits ERRBD to a maximum of 1, which is no loss of generality since a relative error of 1 or more indicates the same thing: a complete loss of accuracy. Note that the value of RCOND returned by xyySVX may apply to a linear system obtained from Ax=b by equilibration, i.e. scaling the rows and columns of A in order to make the condition number smaller. This is the case in the second code fragment in the last section, where the program chose to scale the rows by the factors returned in ${\tt R} = (5.882 \cdot 10^{-5}, .125, .1 )$ and scale the columns by the factors returned in ${\tt C} = (3.333, 1.063, 1. )$ , resulting in ${\tt RCOND} = 3.454 \cdot 10^{-3}$ .

As stated in section 4.3.2, this approach does not respect the presence of zero or tiny entries in A. In contrast, the LAPACK computational routines xyyRFS (subsection 2.4.1) or driver routines xyySVX (subsection 2.3.1) will (except in rare cases) compute a solution $\hat{x}$ with the following properties:

The componentwise backward error of the computed solution $\hat{x}$ is the pair E,f which minimizes

$$\max_{i,j,k} \left( \frac{\vert e_{ij} \vert}{\vert a_{ij}\vert} , \frac{\vert f_{k} \vert}{\vert b_{k}\vert} \right)$$

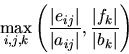
(where we interpret 0/0 as 0) subject to the constraint $(A+E)\hat{x}=b+f$ . The minimal value of $\max_{i,j,k} \left( \frac{\vert e_{ij} \vert}{\vert a_{ij}\vert} , \frac{\vert f_{k} \vert}{\vert b_{k}\vert} \right)$ is given by

$$\omega_{c}= \max_i \frac{\vert r_i\vert}{ (\vert A\vert \cdot \vert\hat{x} \vert + \vert b\vert)_i} \; .$$

One can show that for most problems the $\hat{x}$ computed by xyySVX satisfies $\omega_{c}\leq p(n) \cdot \epsilon$ , where p(n) is a modestly growing function of n. In other words, $\hat{x}$ is the exact solution of the perturbed problem $(A+E)\hat{x}=b+f$ where E and f are small relative perturbations in each entry of A and b, respectively. The corresponding condition number is $\kappa_{c}(A,b,\hat{x}) \equiv {\Vert \, \vert A^{-1}\vert ( \vert A\vert \cdot... ...t{x} \vert + \vert b\vert ) \, \Vert _{\infty}}/{\Vert \hat{x} \Vert _{\infty}}$ . The error $x-\hat{x}$ is bounded by

$$\frac{\Vert x- \hat{x} \Vert _{\infty}}{\Vert \hat{x} \Vert _{\infty}} \leq \omega_{c}\cdot \kappa_{c}(A,b,\hat{x}) .$$

The routines xyyRFS and xyySVX return $\omega_{c}$ , which is called BERR (for Backward ERRor), and a bound on the the actual error $\Vert x - \hat{x}\Vert _{\infty}/ \Vert \hat{x} \Vert _{\infty}$ , called FERR (for Forward ERRor), as in the second code fragment in the last section. FERR is actually calculated by the following formula, which can be smaller than the bound $\omega_{c}\cdot \kappa_{c}(A,b,\hat{x})$ given above:

$$\frac{\Vert x- \hat{x} \Vert _{\infty}}{\Vert \hat{x} \Vert ... ...rt) ) \Vert _{\infty}} {\Vert \hat{x} \Vert _{\infty}} \; \; .$$

Here, $\hat{r}$ is the computed value of the residual $b-A \hat{x}$ , and the norm in the numerator is estimated using the same estimation subroutine used for RCOND.

The value of BERR for the example in the last section is $4.6 \cdot 10^{-8}$ .

Even in the rare cases where xyyRFS fails to make BERR close to its minimum $\epsilon$ , the error bound FERR may remain small. See [6] for details.