Symmetric Eigenproblems (SEP)

The symmetric eigenvalue problem is to find the eigenvalues, 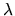$\lambda$ , and corresponding eigenvectors, 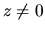$z \ne 0$ , such that

$$Az = \lambda z, \quad A = A^T, \mbox{ where } A \mbox{ is real}.$$

For the Hermitian eigenvalue problem we have

$$Az = \lambda z, \quad A = A^H.$$

For both problems the eigenvalues 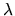$\lambda$ are real.

When all eigenvalues and eigenvectors have been computed, we write:

$$A = Z \Lambda Z^T$$

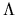where $\Lambda$ is a diagonal matrix whose diagonal elements are the eigenvalues, and Z is an orthogonal (or unitary) matrix whose columns are the eigenvectors. This is the classical spectral factorization of A.

There are four types of driver routines for symmetric and Hermitian eigenproblems. Originally LAPACK had just the simple and expert drivers described below, and the other two were added after improved algorithms were discovered. Ultimately we expect the algorithm in the most recent driver (called RRR below) to supersede all the others, but in LAPACK 3.0 the other drivers may still be faster on some problems, so we retain them.

• A simple driver (name ending -EV) computes all the eigenvalues and (optionally) eigenvectors.

• An expert driver (name ending -EVX) computes all or a selected subset of the eigenvalues and (optionally) eigenvectors. If few enough eigenvalues or eigenvectors are desired, the expert driver is faster than the simple driver.

• A divide-and-conquer driver (name ending -EVD) solves the same problem as the simple driver. It is much faster than the simple driver for large matrices, but uses more workspace. The name divide-and-conquer refers to the underlying algorithm (see sections 2.4.4 and 3.4.3).

• A relatively robust representation (RRR) driver (name ending -EVR) computes all or (in a later release) a subset of the eigenvalues, and (optionally) eigenvectors. It is the fastest algorithm of all (except for a few cases), and uses the least workspace. The name RRR refers to the underlying algorithm (see sections 2.4.4 and 3.4.3).

Different driver routines are provided to take advantage of special structure or storage of the matrix A, as shown in Table 2.5.