Argument Descriptions

The style of the argument descriptions is illustrated by the following example:

N

(input) INTEGER
The number of columns of the matrix A. N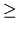 $\geq$ 0.

A

(input/output) REAL array, dimension (LDA,N)
On entry, the m-by-n matrix to be factored.
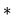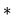On exit, the factors L and U from the factorization A = P$\ast$ L$\ast$ U; the unit diagonal elements of L are not stored.

The description of each argument gives:

• a classification of the argument as (input), (output), (input/output), (input or output)^5.1, (workspace) or (workspace/output)^5.2;

• the type of the argument;

• (for an array) its dimension(s);

• a specification of the value(s) that must be supplied for the argument (if it's an input argument), or of the value(s) returned by the routine (if it's an output argument), or both (if it's an input/output argument). In the last case, the two parts of the description are introduced by the phrases ``On entry'' and ``On exit''.

• (for a scalar input argument) any constraints that the supplied values must satisfy (such as ``N $\geq$ 0'' in the example above).