



Next: Restrictions
Up: Arithmetic Expressions
Previous: Data Type Conversions
Integer division always produces a result which is another integer
value: any fractional part is truncated, i.e. rounded towards zero.
This makes it especially important to provide a decimal point at the
end of a real constant even if the fractional part is zero. For
example:
8 / 3
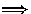
2
-8 / 3
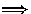
-2
2**(-3)
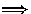
1/(2**3)
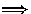
1/8
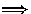
0
The combination of the two preceding rules may have unexpected
effects, for example:
(-2)**3
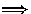
-2 * -2 * -2
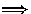
-8
3 / 4 * 5.0
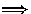
REAL(3/4) * 5.0
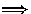
0.0
5.0 * 3 / 4
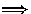
15.0 / REAL(4)
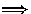
3.75
Helen Rowlands
8/27/1998