



Next: Character comparisons
Up: Relational Expressions
Previous: General Forms of Relational
When the two arithmetic values of differing data type are
compared, a conversion is automatically applied to one of them (as
in arithmetic expressions) to bring it to the type of the other. The
direction of conversion is always:
integer 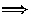 real
real
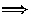 complex
complex or
double precision.
When comparing integer expressions, there is a considerable
difference between the .LE. and .LT. operators, and similarly
between .GE. and .GT., so that you should consider carefully
what
action is required in the limiting case before selecting the
appropriate operator.
In comparisons involving the other arithmetic types you should
remember that the value of a number may not be stored exactly.
This means that it is unwise to rely on tests involving the .EQ. and
.NE. operators except in special cases, for example if one of the
values has previously been set to zero or some other small integer.
There are two restrictions on complex values: firstly they cannot
be compared at all to ones of double precision type. Secondly they
cannot use relational operators other than .EQ. and .NE. because
there is no simple linear ordering of complex numbers.




Next: Character comparisons
Up: Relational Expressions
Previous: General Forms of Relational
Helen Rowlands
8/27/1998